黑洞的定义
黑洞 渐近平直时空$\mathscr{M}$中的黑洞是不属于零未来无限因果过去事件$J^-(\mathscr{T}^+)$的集合
$$\mathscr{B}=\mathscr{M}-J^-(\mathscr{T}^+)$$
视界是区域$\mathscr{B}$的边界
Reissner-Nordström黑洞
赖斯纳-努德斯特伦黑洞是质量为$M$,带电量为$Q$,无旋的黑洞,采用几何单位制,对施瓦西线元进行替换$\displaystyle M\to M-\frac{Q^2}{2r}$可得到其线元
$$\dd s^2=-(1-\frac{2M}{r}+\frac{Q^2}{r^2})\dd t^2+(1-\frac{2M}{r}+\frac{Q^2}{r^2})^{-1}\dd r^2+r^2(\dd \theta^2+\sin^2\theta\dd \phi^2)$$
令$g^{rr}=0$,得到黑洞视界$r_\pm=M\pm\sqrt{M^2-Q^2}$
当$\abs{Q}>\abs{M}$时,视界不存在,$r=0$ 处为裸奇点
Kerr黑洞
克尔黑洞是质量为$M$,不带电,自旋角动量为$J$的黑洞
引入Boyer-Lindquist坐标,比自旋$\displaystyle a=\frac{J}{M}$(无量纲自旋参数$a_*=a/M$),
$\varSigma=r^2+a^2\cos^2\theta$,$\varDelta=r^2-2Mr+a^2$,克尔线元为
$$\dd s^2=-\left(1-\frac{2Mr}{\varSigma}\right)\dd t^2-\frac{4aMr\sin^2\theta}{\varSigma}\dd t\dd \phi+\frac{\varSigma}{\varDelta}\dd r^2+\varSigma\dd\theta^2+\left(r^2+a^2+\frac{2a^2Mr\sin^2\theta}{\varSigma}\right)\sin^2\theta\dd\phi^2$$
令$g^{rr}=0$,得到黑洞视界$r_\pm=M\pm\sqrt{M^2-a^2}$
当$\abs{M}>\abs{a}$时,视界不存在,$r=0$ 处为裸奇点
此度规的
$$\mathscr{H}=\displaystyle\frac{48M^2}{\varSigma^6}(r^6-15a^2r^4\cos^2\theta+15a^4r^2\cos^4\theta-a^6\cos^6\theta)$$
克尔黑洞的时空奇点与无旋黑洞奇点拓扑性质不同,其仅在$\theta=\displaystyle\frac{\pi}{2}$时,即仅在赤道平面具有奇性,此奇点等效于一个圈
沿赤道面之外的测地线能够到达奇点并延伸至另一个$r<0$ 的宇宙,此区域含有闭合的类时曲线,有质量的粒子可以逆时运动
赤道平面的圆轨道
克尔度规位于赤道平面的类时圆轨道对于研究黑洞周围吸积盘结构等天体物理学问题具有重要意义
写出正则形式下克尔线元$\dd s^2=g_{tt}\dd t^2+2g_{t\phi}\dd t\dd \phi+g_{rr}\dd r^2+g_{\theta\theta}\dd\theta^2+g_{\phi\phi}\dd\phi^2$
$m=1$的自由粒子拉格朗日量$L=\displaystyle\frac{1}{2}g_{\mu\nu}\dot{x}^\mu\dot{x}^\nu$与$t,\phi$无关
故有守恒量 $p_t=g_{tt}\dot{t}+g_{t\phi}\dot{\phi}=-E$,$p_\phi=g_{t\phi}+g_{\phi\phi}=L_z$,$E$为无穷远处比能量,$L$为无穷远处比角动量的轴向分量
由$g_{\mu\nu}\dot{x}^\mu\dot{x}^\nu=-1$引入有效势$V_\text{eff}(r,\theta)$,
$g_{rr}\dot{r}^2+g_{\theta\theta}\dot{\theta}^2=V_\text{eff}=\displaystyle\frac{E^2 g_{\phi\phi}+2EL_zg_{t\phi}+L_z^2g_{tt}}{g_{t\phi}^2-g_{tt}g_{\phi\phi}}-1$
赤道圆轨道位于有效势的驻点,意味着$V_\text{eff},\partial_rV_\text{eff},\partial_\theta V_\text{eff}=0$,由这些条件可以解出守恒量$E,L_z$,但下面可以用测地线方程更为方便地求解
测地线方程$\displaystyle\frac{\dd}{\dd \tau}(g_{\mu\nu}\dot{x}^\nu)=\frac{1}{2}\partial_\mu g_{\nu\rho}\dot{x}^\nu\dot{x}^\rho$,将赤道圆轨道条件$\dot{r},\dot{\theta}=0$ 代入有
径向分量 $\partial_r g_{tt}\dot{t}^2+2\partial_r g_{t\phi}\dot{t}\dot{\phi}+\partial_r g_{\phi\phi}\dot{\phi}^2=0$,
解得角速度 $\Omega_{\pm}=\displaystyle\frac{\dot{\phi}}{\dot{t}}=\pm\frac{M^{1/2}}{r^{3/2}\pm aM^{1/2}}$,正负号分别代表共旋与对旋轨道
又由$g_{tt}\dot{t}^2+2g_{t\phi}\dot{t}\dot{\phi}+g_{\phi\phi}\dot{\phi}^2=-1$得$\dot{t}=\displaystyle\frac{1}{\sqrt{-g_{tt}-2\Omega g_{t\phi}-\Omega^2g_{\phi\phi}}}$
代入守恒量$E,L_z$表达式
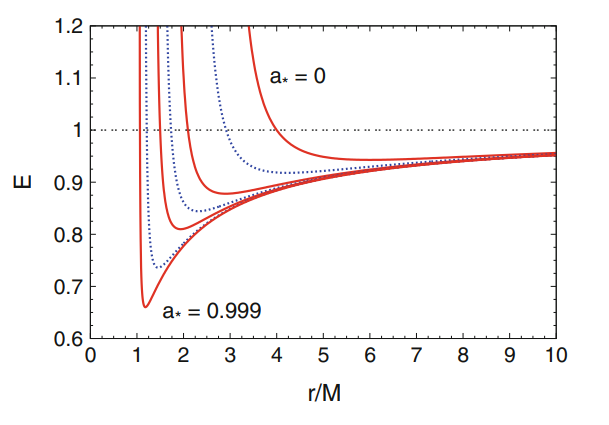
$E=-\displaystyle\frac{g_{tt}+\Omega g_{t\phi}}{\sqrt{-g_{tt}-2\Omega g_{t\phi}-\Omega^2g_{\phi\phi}}}=\frac{r^{3/2}-2Mr^{1/2}\pm aM^{1/2}}{r^{3/4}\sqrt{r^{3/2}-3Mr^{1/2}\pm 2aM^{1/2}}}$,
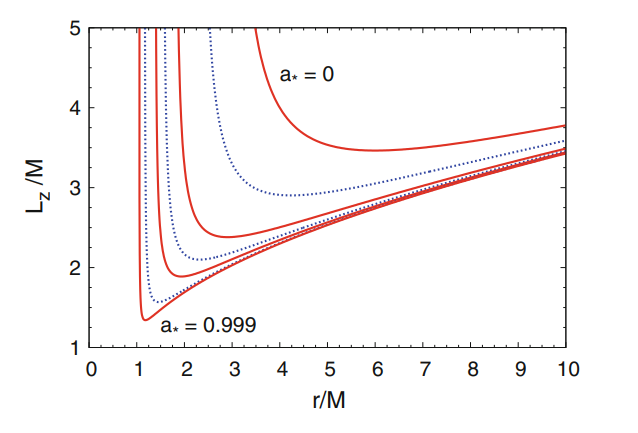
$L_z=\displaystyle\frac{g_{t\phi}+\Omega g_{\phi\phi}}{\sqrt{-g_{tt}-2\Omega g_{t\phi}-\Omega^2g_{\phi\phi}}}=\pm\frac{M^{1/2}(r^{2}\mp 2aM^{1/2}r^{1/2}+ a^2)}{r^{3/4}\sqrt{r^{3/2}-3Mr^{1/2}\pm 2aM^{1/2}}}$
 |
 |
|---|
在光子轨道 $\displaystyle r_{\gamma\pm}=2M\left\lbrace 1+\cos\left[\frac{2}{3}\arccos\left(\mp\frac{a}{M}\right)\right]\right\rbrace$ 处,$E,L_z$发散
当$a=0$时,$r_\gamma=3M$;
当$a=M$时,$r_{\gamma +}=M,r_{\gamma -}=4M$
在边缘束缚轨道 $r_{\text{mb}\pm}=2M\mp a+2\sqrt{M(M\mp a)}$处,粒子刚好具备逃逸所需能量$E=1$,$r<r_{\text{mb}}$之内圆轨道上运动的粒子能够逃逸,反之将被束缚
当$a=0$时,$r_\gamma=4M$;
当$a=M$时,$r_{\gamma +}=M,r_{\gamma -}=(3+2\sqrt{2}M)\approx 5.83M$
边缘稳定轨道,又称最内稳定圆轨道
$r_{\text{ISCO}\pm}=3M+Z_2\mp \sqrt{(3M-Z_1)(3M+Z_1+2Z_2)}$
$Z_1=M+(M^2-a^2)^{1/3}[(M+a)^{1/3}+(M-a)^{1/3}],Z_2=\sqrt{3a^2+Z_1^2}$
在此处,$\partial_r^2 V_\text{eff},\partial_\theta^2 V_\text{eff}=0$,$E$与$L_z$同时取到极小值,$r<r_{\text{ISCO}}$的圆轨道是径向不稳定的,但克尔度规中的圆轨道总是垂直稳定的
当$a=0$时,$r_{\text{ISCO}}=6M$;
当$a=M$时,$r_{\text{ISCO}+}=M,r_{\text{ISCO}-}=9M$
| 视界$r_+$,光子轨道$r_\gamma$,边缘束缚轨道$r_\text{mb}$,最稳定内圆轨道$r_\text{ISCO}$随自旋参数$a_*$变化曲线 |
|---|
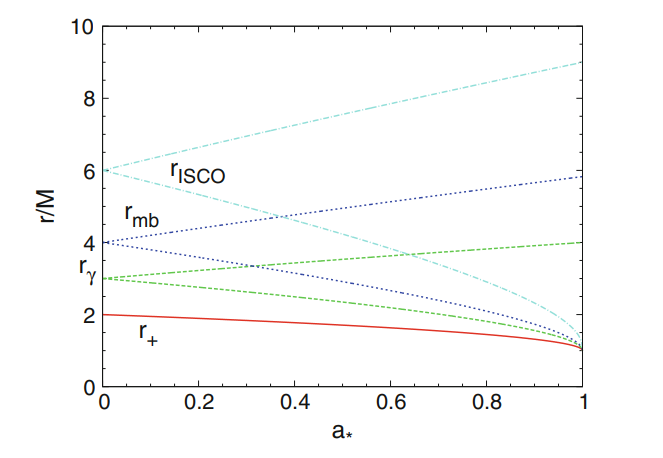 |
虽然$a=M$的极端克尔黑洞条件下,$r_+=r_{\gamma +}=r_\text{mb+}=r_\text{ISCO+}=M$,但是在视界处伯耶-林奎斯特坐标在视界处没有明确定义,令$a=M(1-\varepsilon)$并令$\varepsilon\to 0$
$r_+=M(1+\sqrt{2\varepsilon}+O(\varepsilon))$,$r_{\gamma+}=\displaystyle M\left(1+2\sqrt{\frac{2\varepsilon}{3}}+O(\varepsilon)\right)$
$r_\text{mb+}=M(1+2\sqrt{\varepsilon}+O(\varepsilon))$,$r_\text{ISCO+}=M[1+(4\varepsilon)^{1/3}+O(\varepsilon)]$
$r_+$与其他轨道之间的固有径向距离为
$\displaystyle\int_{r_+}^{r_{\gamma +} }\frac{r’\dd r’}{\sqrt{\varDelta}}\to \frac{1}{2}M\ln{3}$,
$\displaystyle\int_{r_+}^{r_\text{mb +} }\frac{r’\dd r’}{\sqrt{\varDelta}}\to M\ln(1+\sqrt{2})$,
$\displaystyle\int_{r_+}^{r_\text{ISCO +} }\frac{r’\dd r’}{\sqrt{\varDelta}}\to \frac{1}{6}M\ln\left(\frac{2^7}{\varepsilon}\right)$
虽然在伯耶-林奎斯特坐标下这些轨道半径相同,但其并不重合
在除视界之外的轨道上能量与角动量为
$r_\gamma: E\to \infty,L_z\to 2EM$,
$r_\text{mb}: E\to 1,L_z\to 2M$,
$r_\text{ISCO}:E\to \displaystyle\frac{1}{\sqrt{3}},L_z\to \frac{2}{\sqrt{3}}M$
基频
赤道圆轨道由轨道频率$\nu_\phi$,径向本轮频率$\nu_r$,垂直本轮频率$\nu_\theta$三个基频描述,
牛顿引力下三个基频相等,$\nu_\phi=\nu_r=\nu_\theta=\displaystyle\frac{1}{2\pi}\frac{M^{1/2}}{r^{3/2}}$
施瓦西度规下具有牛顿引力中不具有的最稳定内圆轨道与光子轨道,由于$r<r_\text{ISCO}$时圆轨道径向不稳定,故径向本轮频率$\nu_r$在$r_\text{ISCO}$处为零;而轨道频率和垂直本轮频率可以向内取到光子轨道处,这三个基频随自旋参数的变化关系如图所示
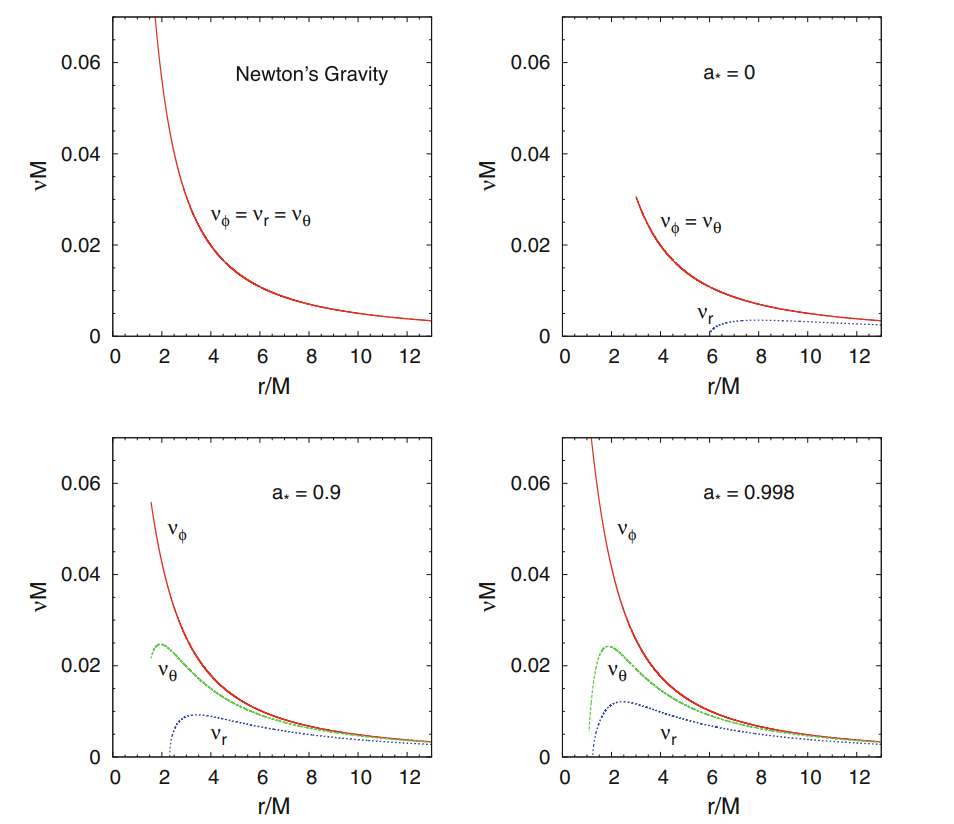
$\nu_\phi=|\Omega|/(2\pi)$,而通过附加微扰可以得到$\nu_\theta,\nu_r$表达式
$\displaystyle\nu_\phi=\frac{1}{2\pi}\frac{M^{1/2}}{r^{3/2}\pm aM^{1/2}}$,
$\displaystyle\nu_\theta=\nu_\phi\sqrt{1\mp \frac{4aM^{1/2}}{r^{3/2}}+\frac{3a^2}{r^2}}$
$\nu_r=\displaystyle\nu_\phi\sqrt{1-\frac{6M}{r}\pm \frac{8aM^{1/2}}{r^{3/2}}-\frac{3a^2}{r^2}}$
施瓦西黑洞轨道频率为$\displaystyle\nu_\phi(a_*=0)\approx 220\left(\frac{M_\odot}{M}\right)\left(\frac{6M}{r}\right)^{3/2} \text{Hz}$
一个太阳质量的施瓦西黑洞在最稳内圆轨道处的轨道频率$\nu_\phi\approx 2200\text{Hz}$
参考系拖曳
从共旋与对旋轨道粒子角速度不同可知,产生引力场的自旋体迫使周围物质绕其同向旋转,亦即自旋体拖曳周围时空随之转动,即使粒子角动量为零,其仍可以非零的角速度在克尔黑洞周围轨道运动,
令$L_z=g_{t\phi}\dot{t}+g_{\phi\phi}\dot{\phi}=0$,则有 $\Omega=-\displaystyle\frac{g_{t\phi}}{g_{\phi\phi}}=\frac{2Mar}{(r^2+a^2)\varSigma+2Ma^2r\sin^2\theta}$
视界角速度 $\Omega_H=-\displaystyle\left(\frac{g_{t\phi}}{g_{\phi\phi}}\right)_{r=r_+}=\frac{a_*}{2r_+}$
静态极限为$g_{tt}=0$的表面,其半径 $r_\text{sl}=M+\sqrt{M^2-a^2\cos^2\theta}$,视界与静态极限中间区域$g_{tt}>0$ 称为能层,
由于静止粒子线元$\dd s^2=g_{tt}\dd t^2$,在能层中其将对应$\dd s^2>0$ 的类空轨迹,这是不被允许的,故能层中不存在静止粒子,一切都在旋转
无毛定理
对克尔度规作替换$M\to \displaystyle M-\frac{Q^2}{2r}$,得到Ker-Newman度规,其描述仅由质量$M$,电荷量$Q$,自旋角动量$J$三个参数决定的黑洞,
克尔-纽曼度规是四维电磁真空中爱因斯坦方程恒定、轴对称、渐近平直且规则的唯一解,这是无毛定理的结果,其表明黑洞除$M,Q,J$之外不具有其他特征,但是放宽条件或者在爱因斯坦引力的推广下无毛定理是可以被违背的
引力坍缩
当恒星耗尽燃料,气体压强无法抗衡引力,其将收缩为白矮星,由简并电子压强平衡引力;若质量超过Chandrasekhar极限($1.44M_\odot$),其将继续坍缩为中子星,由简并中子压强平衡引力;若质量超过Oppenheimer极限($2\sim 3 M_\odot$),则将坍缩为黑洞
考虑球对称坍缩,一般度规$g_{\mu\nu}=\text{diag}(-e^{2\lambda},e^{2\psi},R^2,R^2\sin^2\theta)$,$\lambda,\psi,R$仅为$t,r$的函数,
选取共动参考系,即坐标附着在每个坍缩粒子上,在坍缩过程中始终保持每个粒子的$r$不变,粒子在此参考系内的四维速度为$u^\mu=(e^{-\lambda},0,0,0)$
设坍缩体为理想流体,在共动参考系即坍缩流体静止系中其能动张量$T_\nu^\mu=\text{diag}(-\rho,P,P,P)$,
由度规计算爱因斯坦张量,以下 $\dot{x}=\dd x/\dd t,x’=\dd x/\dd r$,
Misner—Sharp质量$F=R(1-e^{-2\psi}R’^2+e^{-2\lambda}\dot{R}^2)$,
其定义为$\displaystyle 1-\frac{F}{R}=g_{\mu\nu}\partial^\mu R\partial ^\nu R$,爱因斯坦张量可表示为
$G_t^t=-\displaystyle\frac{F’}{R^2R’}+\frac{2\dot{R}e^{-2\lambda}}{RR’}(\dot{R}’-\dot{R}\lambda’-\dot{\psi}R’)$
$G_r^r=-\displaystyle\frac{\dot{F}}{R^2\dot{R}}-\frac{2R’e^{-2\psi}}{R\dot{R}}(\dot{R}’-\dot{R}\lambda’-\dot{\psi}R’)$
$G_r^t=-e^{2\psi-2\lambda}G_t^r=\displaystyle\frac{2e^{-2\lambda}}{R}(\dot{R}’-\dot{R}\lambda’-\dot{\psi}R’)$
$$\begin{aligned} G_\theta^\theta=\displaystyle G_\phi^\phi&=\frac{e^{-2\psi}}{R}[(\lambda’’+\lambda’^2-\lambda’\psi’)R+R’’+R’\lambda’-R’\lambda’]\\
&-\displaystyle\frac{e^{-2\lambda}}{R}[(\ddot{\psi}+\dot{\psi}^2-\dot{\lambda}\dot{\psi})R+\ddot{R}+\dot{R}\dot{\psi}-\dot{R}\dot{\lambda}]\end{aligned}$$
代入爱因斯坦方程$G_\mu^\nu=8\pi T_\mu^\nu$
$$\dot{R}’-\dot{R}\lambda’-\dot{\psi}R’=0 \tag{1} \label{eq1}$$
$$\displaystyle\frac{F’}{R^2R’}=8\pi\rho \tag{2} \label{eq2}$$
$$\displaystyle\frac{\dot{F}}{R^2\dot{R}}=-8\pi P \tag{3} \label{eq3}$$
由$\eqref{eq1}$计算半径$r$以内米斯纳-夏普质量 ,可以发现其正比于引力质量
$F(r)=\displaystyle \int_0^r F’\dd $$\displaystyle\tilde{r}=8\pi\int_0^r \rho R^2 R’ \tilde{r}=2M(r)$
而由$\nabla_\mu T_\nu^\mu=0$ 可得第四个关系式
$$\lambda’=-\displaystyle\frac{P’}{\rho+P}\tag{4}\label{eq4}$$
尘埃坍缩
考虑物态方程$P=0$(尘埃)的情况,由$\eqref{eq3}$,$\eqref{eq4}$有 $\dot{F}=0,\lambda’=0$
$F=F(r)$独立于$t$意味着没有穿过球壳的质量流,
$\lambda=\lambda(t)$独立于$r$,则可以选取新的时间坐标$\tilde{t}$,使得$\dd $$\tilde{t}=e^\lambda\dd t$,新时间规范下$\lambda=0$,$g_{\tilde{t}\tilde{t}}=-1$,
由$\eqref{eq1}$有$\dot{R}’-\dot{\psi}R’=0$,可得$\displaystyle R’=e^{g(r)+\psi}$,
引入$f(r)=e^{2g(r)}-1$,由米斯纳-夏普质量表达式,$\dot{R}^2=\displaystyle\frac{F}{R}+f$,得到Lemaitre-Tolman-Bondi度规,其线元为
$$\dd s^2=-\dd t^2+\displaystyle\frac{R’^2}{1+f}\dd r^2+ R^2(\dd \theta^2+\sin\theta^2\dd \phi^2)$$
克莱舒曼标量$\mathscr{H}=12\displaystyle\frac{F’^2}{R^4R’^2}-32\frac{FF’}{R^5R’}+48\frac{F^2}{R^6}$
当$R=0$时$\mathscr{H}$发散,尘埃坍缩成奇点,
系统拥有一个可通过设定某一特定时间的标度来固定的规范自由度,故设$R(t,r)=ra(t,r)$,$a$为标度因子,$a(0,r)=1$,坍缩条件要求$\dot{a}<0$,奇点时刻$a=0$
由初始时刻能量密度的规则性可令$F(r)=r^3m(r)$,$m(r)$为$[0,r_b]$上的规则函数,$m(r)=\displaystyle\sum_{k=0}^\infty m_k r^k$,能量密度在$r=0$处平缓变化要求$m_1=0$
$\eqref{eq2}$成为$\rho=\displaystyle\frac{3m+rm’}{a^2(a+ra’)}$
若$m’\neq 0,R’=0$,克莱舒曼标量仍然发散,但其对应的奇点于$R=0$的奇点本质上是不同的,这些奇点产生于径向壳层重叠,称为壳层交叉奇点,在重叠壳层处径向测地距离为零,但通过定义合适的坐标,时空可以延拓到这些奇点处,因此不妨要求$R’\neq 0$或$m’/R’$不发散
$\dot{R}^2=\displaystyle\frac{F}{R}+f$ 成为 $\dot{a}(0,r)=-\displaystyle\sqrt{m+\frac{f}{r^2}}$,可见$f$决定坍缩尘埃的初速度分布,为使坍缩速度有限,需对$f$施加限制,普遍写作$f(r)=r^2b(r)$,$b(r)=\displaystyle\sum_k^\infty b_k r^k$
均匀尘埃坍缩
Oppenheimer-Snyder模型描述均匀球对称尘埃云坍缩,尘埃密度$\rho=\rho(t)$独立于$r$,坍缩速度$r\dot{a}$正比于$r$,故$m=m_0,b=b_0$,$\displaystyle\dot{a}(t)=\sqrt{\frac{m_0}{a}+b_0}$,线元成为
$$\dd s^2=-\dd t^2+a^2\left(\frac{\dd r^2}{1+b_0r^2}+r^2\dd\theta^2+r^2\sin^2\theta^2\dd \phi^2\right)$$
令$b_0=0$,对应边缘束缚坍缩,即无穷远处粒子坍缩速度为零,
可解得$a(t)=\displaystyle\left(1-\frac{3\sqrt{m_0}}{2}t\right)^{2/3}$,奇点形成时刻$t_s=\displaystyle\frac{2}{3\sqrt{m_0}}$
表观视界可以理解为向外指向的光线逃脱引力向外运动和被引力俘获而向内运动的分界面,令表观视界与壳层$r$重合的时刻为$t_\text{ah}(r)$,此时坍缩速度等于光速,$r\dot{a}=1$,令$b_0=0$,可解得$t_\text{ah}=\displaystyle\frac{2}{3\sqrt{m_0}}-\frac{2}{3}r^3m_0$
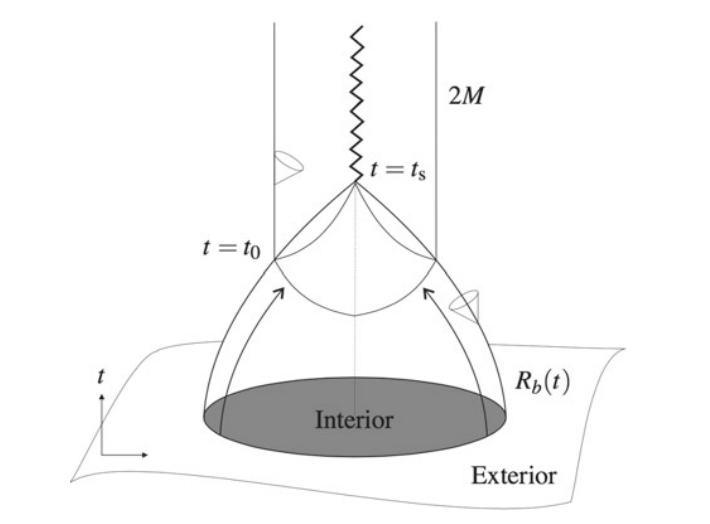
以下Finkelstein图描述了球对称尘埃云的引力坍缩过程,在$t=t_0$时刻尘埃云表面穿入施瓦西半径,同时外部区域的视界和位于边界$r_b$处的表观视界形成,即$t_0=t_\text{ah}(r_b)$,此后外部区域为静态施瓦西时空,表观视界的半径逐渐缩小,并在$t_s$时刻到达奇点$r=0$ 处
Penrose Diagram
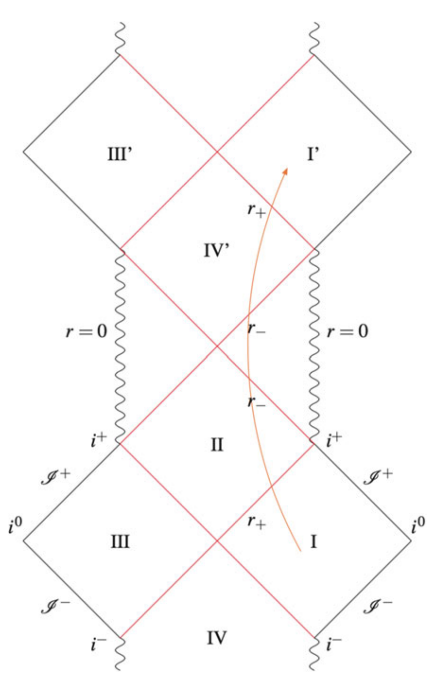
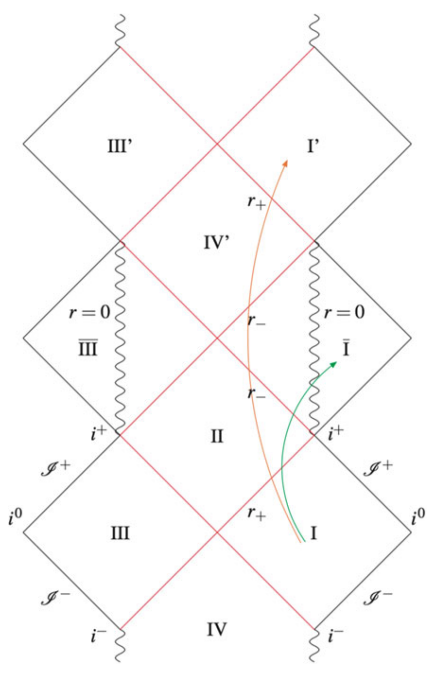
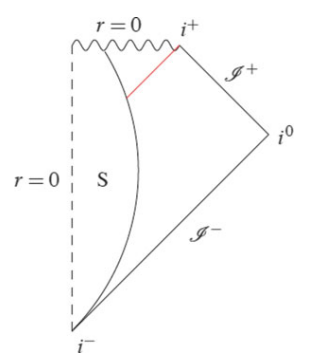
以下分别为赖斯纳-努德斯特伦时空、克尔时空和奥本海默-史奈德时空的最大延拓彭罗斯图
 |
 |
 |
|---|
From Cosmo Bambi’s Introduction to General Relativity