向量丛
$M$上秩为$r$的向量丛为配备光滑丛投影$\pi: E\to M$的光滑流形$E$,并满足
$1.$ $\forall p\in M$,纤维$\pi^{-1}(p)=E_p$为$r$维向量空间
$2.$ $\forall p\in M$,存在开邻域$U\subseteq M$与微分同胚$t:E_U=\pi^{-1}(U)\to U\times \mathbb{R}^r$
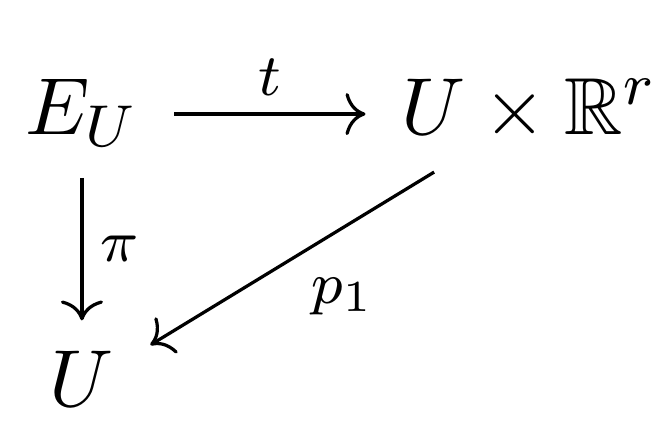
称$E$为丛空间,$M$为底空间,$t$为$E$在$U$上的局部平凡化,秩为$1$的向量丛称为线丛
设$t_\alpha$与$t_\beta$为$E$的局部平凡化,则$t_\alpha\circ t_\beta^{-1}:(U_\alpha \bigcap U_\beta)\times \mathbb{R}^r\to (U_\alpha \bigcap U_\beta)\times \mathbb{R}^r$为纤维上的线性变换
$$t_\alpha\circ t_\beta^{-1}(p,v)=(p,g_{\alpha\beta}(p)v),\qquad g_{\alpha\beta}:U_\alpha \bigcap U_\beta \to GL(r,\mathbb{R})$$
称$g_{\alpha\beta}$为$\beta$到$\alpha$的转移函数,其满足
$g_{\alpha\alpha}=\text{id}$
$g_{\alpha\beta}=g_{\beta\alpha}^{-1}$
$g_{\alpha\beta}g_{\beta\gamma}g_{\gamma\alpha}=\text{id}$
向量丛$\pi: E\to M$的一个截面为映射$s:M\to E,\pi\circ s=\text{id}$,$\forall p\in M,s(p)\in E_p$,记$E$的截面族为$\Gamma(M,E)$
由以下交换图定义丛映射$F:E\to E’,f:M\to M’$,使得$\forall p\in M$,$F_p:E_p\to E’_{f(p)}$为线性变换
$$
\begin{CD}
E @>F>> E’\\
@V\pi VV @V\pi’VV\\
M @>f>> M’
\end{CD}$$
若两个向量丛基空间均为$M$,并存在建立在$\text{id}_M$上的丛映射$E_1\to E_2$,则称其同构$E_1\cong E_2$,任何向量空间的操作都可以通过对纤维的作用引入向量丛
定义向量丛$\pi: E\to M$,$\rho: F\to M$的Whitney和
$$E\oplus F=\lbrace(e,f)\in E\times F:\pi(e)=\rho(f)\rbrace$$
其自然诱导出向量丛$\pi\oplus\rho:E\oplus F\to M$,满足$\pi\oplus\rho(e,f)=\pi(e)=\rho(f)$
定义$M$上向量丛$E,F$的张量积
$$(E\otimes F)|_p=E_p\otimes F_p$$
同理可定义交错积$\bigwedge^n E$
定义对偶向量丛
$$E^*=\bigcup_{p\in M}E_p^*$$
设$t_\alpha$为$E$的局部平凡化$t_\alpha:E|_{U_\alpha}\to U_\alpha\times \mathbb{R}^r$,
则有对偶$ t_\alpha^*:U_\alpha\times(\mathbb{R}^{n})^* \to E|_{U_\alpha}^*$,由于$(\mathbb{R}^{n})^*\cong \mathbb{R}^{n}$,
故有$E^*$的局部平凡化$E|_{U_\alpha}^*\to U_\alpha\times \mathbb{R}^r$
定义向量丛$\pi:E\to M$的拉回,$f:N\to M$
$$f^*E=\lbrace(y,e)\in N\times E:f(y)=\pi(e)\rbrace$$
取投影为$(y,e)\mapsto y$,得到$N$上向量丛$f^*\pi:f^*E\to N$,$(f^*E)_y=E_{f(y)}$,并可诱导出$N$上向量丛的局部平凡化
对$M$上两个向量丛$E,F$,若$F$为$E$子流形,即$\forall p\in M$,纤维$F_p$为$E_p$子空间,则称$F$为$E$的子丛,由子丛可定义商丛
$$\pi:E/F=\bigcup_{p\in M}E_p/F_p\to M$$
若$f:M\hookrightarrow N$为嵌入,则$TM\to M$为$f^* TN\to M$的子丛,
商丛$f^* TN/TM\to M$称为$M$的法丛
令$V$为向量空间,$G$为李群,$\rho: G\to GL(V)$为群表示,
由以下条件定义G-丛
$1.$ $\forall p\in M,\pi^{-1}(p)\cong V$
$2.$ 存在局部平凡化覆盖$\lbrace U_\alpha\rbrace$与转移函数$g_{\alpha\beta}:(U_\alpha \bigcap U_\beta)\times V\to (U_\alpha \bigcap U_\beta)\times V$
$3.$ 转移函数由映射$g_{\alpha\beta}:U_\alpha \bigcap U_\beta\to G$和群表示$\rho$复合构造,$g_{\alpha\beta}=\rho\circ g_{\alpha\beta}$
G-主丛
令$G$为李群,$M$上的G-主丛为配备光滑丛投影$\pi: P\to M$的光滑流形$P$,并满足
$1.$ $\forall x\in M$,纤维$\pi^{-1}(x)\cong G$
$2.$ $\forall x\in M$,存在开邻域$U\subseteq M$与微分同胚$t:\pi^{-1}(U)\to U\times G$
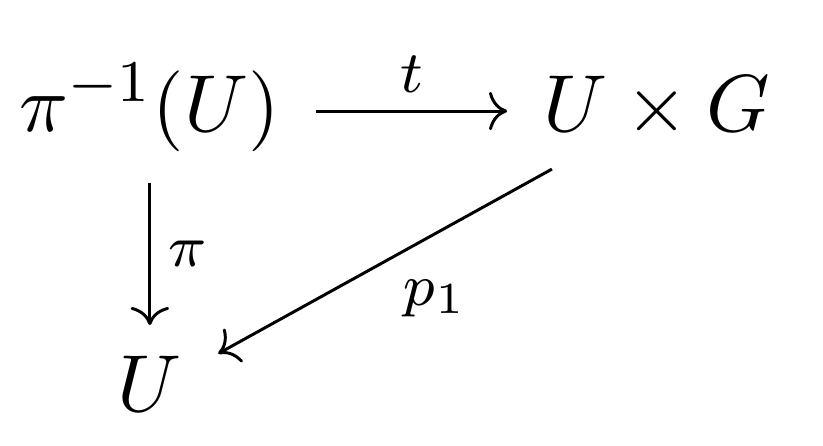
可由局部平凡化定义转移函数,$t_\alpha\circ t_\beta^{-1}:(U_\alpha \bigcap U_\beta)\times G\to (U_\alpha \bigcap U_\beta)\times G$
$$(x,g)\mapsto (x,g_{\alpha\beta}(x)\cdot g)\qquad g_{\alpha\beta}(x):U_\alpha \bigcap U_\beta\to G$$
$G$称为结构群,转移函数满足向量丛转移函数的三个性质
给出$G$的表示$\rho: G\to GL(V)$,考虑$G$作用于$P\times V$
$$(u,y)\mapsto (ug,\rho(g)^{-1}y)$$
可定义G-主丛的关联向量丛,$E=P\times_\rho V:=(P\times V)/G$
联络与曲率
向量丛$\pi: E\to M$上的联络为双线性映射
$$\nabla:\mathfrak{X}(M)\times \Gamma(E)\to \Gamma(E); (X,s)\mapsto \nabla_X s$$
其满足
$1.$ $\nabla_{fX}(s)=f\nabla_Xs$
$2.$ 莱布尼茨律 $\nabla_X(fs)=Xf(s)+f(\nabla_Xs)$
若向量丛$E$具有度规$g$,则称满足以下条件的联络与此度规适配
$$Xg(s_1,s_2)=g(\nabla_X s_1,s_2)+g(s_1,\nabla_X s_2)$$
向量丛$\pi: E\to M$上的曲率为三线性映射
$$F:\mathfrak{X}(M)\times \mathfrak{X}(M)\times\Gamma(E)\to \Gamma(E); (X,Y,s)\mapsto F(X,Y)s$$
$$F(X,Y)s=(\nabla_X\nabla_Y-\nabla_Y\nabla_X-\nabla_{[X,Y]})s$$
其满足
$1.$ $F(X,Y)s=-F(Y,X)s$
$2.$ $\forall f,g,h\in C^\infty(M),\;F(fX,gY)(hs)=fghF(X,Y)s$
联络可在局部坐标系$s_1,s_2,\cdots,s_r\in \Gamma(\pi^{-1}(U))$下写为$\nabla_Xs_j=\displaystyle\sum_{i=1}^r s_iA_{\;j}^i(X)$,
$A_{\;j}^i\in \Omega^1(U,\mathfrak{gl}(r,\mathbb{R}))$称为联络形式
曲率可写为$F(X,Y)s_j=\displaystyle\sum_{i=1}^r s_iF_{\;j}^i(X,Y)$
$F_{\;j}^i\in \Omega^2(U,\mathfrak{gl}(r,\mathbb{R}))$称为曲率形式
联络形式与曲率形式有关系
$$F=\dd A+A\wedge A$$
曲率形式满足Bianchi恒等式 $\dd F- F\wedge A+ A\wedge F=0$
将截面$s$用基展开,$s=\displaystyle\sum_{j=1}^r v^j(x)s_j$,联络和曲率分量在局部坐标系下可表示为
$$\nabla_{\frac{\partial}{\partial x^\mu}}s=\displaystyle\sum_{i=1}^rs_i\left[\frac{\partial v^i(x)}{\partial x^\mu}+(A_\mu)_{\;j}^i v^j(x)\right]$$
$$F(\frac{\partial}{\partial x^\mu},\frac{\partial}{\partial x^\nu})=F_{\mu\nu}=\frac{\partial A_\nu}{\partial x^\mu}-\frac{\partial A_\mu}{\partial x^\nu}+[A_\mu,A_\nu]$$
在Maxwell $\text{U(1)}$ 理论中,$[A_\mu,A_\nu]=0$
给定转移函数$g_{\alpha\beta}:U_\alpha\bigcap U_\beta\to GL(r,\mathbb{R})$,则$U_\alpha$和$U_\beta$上有关系
$$A_\beta=g_{\alpha\beta}^{-1}A_\alpha g_{\alpha\beta}+g_{\alpha\beta}^{-1}\dd(g_{\alpha\beta})$$
$$F_\beta=g_{\alpha\beta}^{-1}F_\alpha g_{\alpha\beta}$$
对于$G$丛,将$g_{\alpha\beta}$用群表示代替,$\dd(g_{\alpha\beta})$用Maurer-Cartan形式代替
在麦克斯韦理论中,规范变换为$g_{\alpha\beta}=e^{i\lambda_{\alpha\beta}}$,对应$A_\beta=A_\alpha+i\dd \lambda_{\alpha\beta}$
平移与和乐群
给定截面$s\in \Gamma(E)$与道路$\gamma:I\to M$,若$s$满足如下条件则称其在$\gamma$上平行
$$\nabla_{\dot{\gamma}(t)}s=0\qquad \forall\;t\in I$$
在局部坐标系下可写作
$$\frac{\dd s_i}{\dd t}+\sum_{i=1}^rs_j(A_\mu)_{\; i}^j\frac{\dd x^\mu}{\dd t}=0$$
由平移可定义映射$\tau_\gamma:E_{\gamma(0)} \ni s(t=0) \to s(t=1)\in E_{\gamma(1)}$
若考虑闭合曲线$\gamma(0)=\gamma(1)=p$,则得到映射$\tau_\gamma:E_p\to E_p$
定义积和逆为$\tau_{\gamma_1}\circ\tau_{\gamma_2}=\tau_{\gamma_1\circ \gamma_2},\;\tau_\gamma^{-1}=\tau_{\gamma^{-1}}$,
如此定义的映射构成Holonomy Group
在$U(1)$丛中,这是Aharonov-Bohm效应的起源,考虑如下形式的波函数,易知其在$\gamma$上平行
$$s(t):=s(0)\exp(-\int_{\gamma(t)}A)=s(0)\exp(-\int A_\mu\frac{\dd x^\mu}{\dd t}\dd t)$$
规范变换$A_\beta=A_\alpha+i\dd \lambda_{\alpha\beta}$对$s(t)$的相位有影响
Levi-Civita联络
考虑配备黎曼度规$g$的切丛$TM$,则可自然诱导出$TM$上唯一与$g$适配的联络,称为列维-奇维塔联络
对于列维-奇维塔联络可以写出
$$\nabla_{X_j}X_i=\sum_{k}\Gamma_{ij}^kX_k\qquad R(X_i,X_j)X_k=\sum_{l}R_{\;kij}^lX_l$$
联络与曲率形式
$$\omega_{\;j}^k=\sum_{i}\Gamma_{ij}^ke^i\qquad\Omega_{\;k}^l=\sum_{i,j}R_{\;kij}^le^i\wedge e^j$$
满足条件
$$\dd e^i=-\sum_{j}\omega_{\;j}^i\wedge e^j\qquad\Omega_{\;j}^i=\dd\omega_{\;j}^i+\omega_{\;k}^i\wedge\omega_{\;j}^k$$
Ehresmann联络
G-主丛$\pi:P\to M$上的埃雷斯曼联络为满足以下条件的1-形式$A\in \Omega^1(P,\mathfrak{g})$
$1.$ 对$X\in\mathfrak{g}$,令$\overline{X}_u=\displaystyle\frac{\dd}{\dd t}(u\cdot\exp{tX})|_u\quad u\in P$,有$A(\overline{X})=X$
$2.$ $\forall\; g\in G$,对右作用$R_g$有$R_g^*(A)=\text{ad}(g^{-1})A$,即
$$A_{ug}(R_g(Y))=\text{ad}(g^{-1})(A_u(Y))=g^{-1}(A_u(Y))g\quad\forall\; Y\in T_uP$$
对于局部平凡化$P_U\to U\times G$,$P$在$u$处切空间$T_uP$可以划分为与$U$相切的水平成分$H_uP$和于$G$相切的垂直成分$V_uP$,由上定义的埃雷斯曼联络的核即为切空间$T_uP$的水平子空间$H_uP=\lbrace X\in T_uP \;|\; A(X)=0\rbrace$,
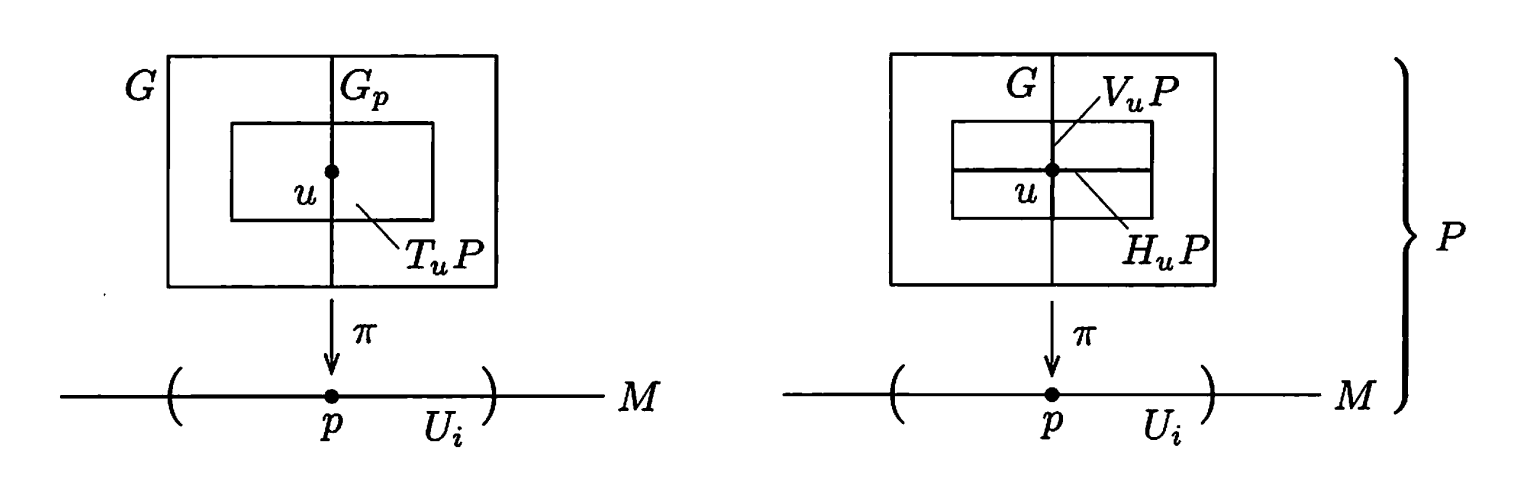
并且$H_uP$在右作用下仍保持为水平子空间$R_{g*}H_uP=H_{ug}P$
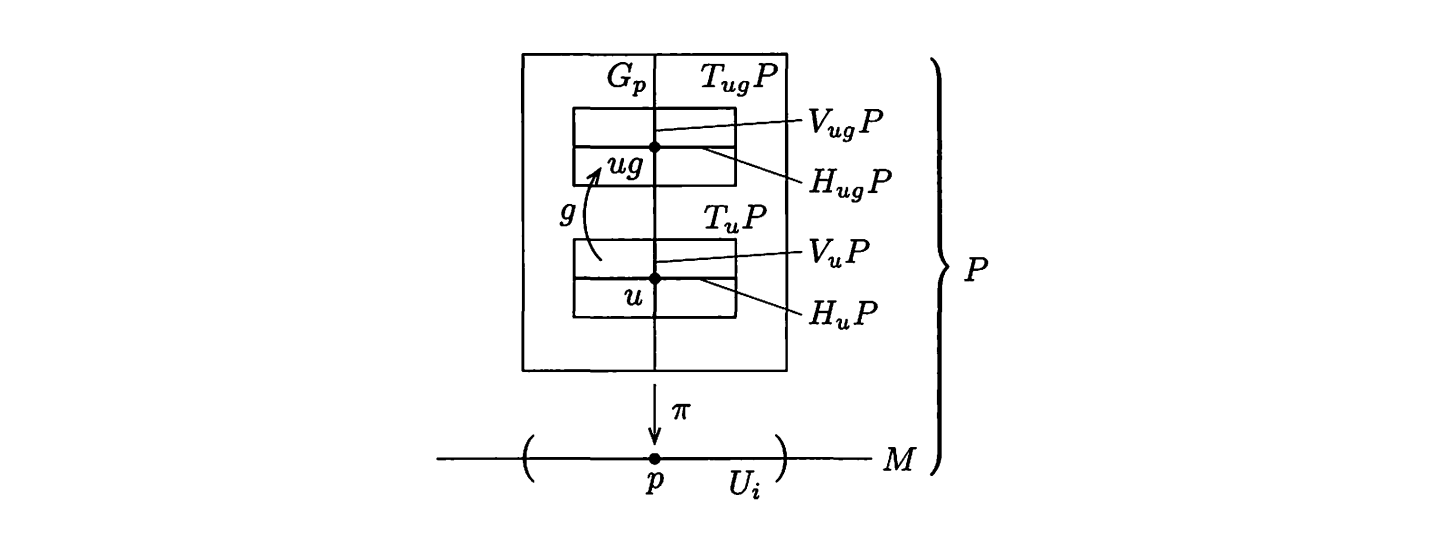
由局部平凡化$t_\alpha:\pi^{-1}(U_\alpha)\to U_\alpha\times G$,可得$\pi^{-1}(U_\alpha)$上截面
$$s_\alpha:U_\alpha\to P\;;\; p\mapsto t_\alpha^{-1}(p,e)$$
再用截面将埃雷斯曼联络拉回$M$上,$A_\alpha=s_{\alpha}^*(A)$,在$M$上有规范变换
$$A_\beta=g_{\alpha\beta}^{-1}A_\alpha g_{\alpha\beta}+g_{\alpha\beta}^{-1}\dd(g_{\alpha\beta})\quad \text{for} \; U_\alpha\bigcap U_\beta$$
将埃雷斯曼联络空间记为$\mathscr{A}_P$,规范变换空间为$G_P:=P\times_{\text{Ad}} G$ 的截面族$\Gamma(M,G_P)$,记为$\mathscr{G}_P$,将规范变换$g\in\mathscr{G}_P$作用于$\mathscr{A}_P$
$$\mathscr{G}_P\times \mathscr{A}_P\to \mathscr{A}_P\; ;\; (g,A)\mapsto g^*(A)=\lbrace g^*(A)_U,g^*(A)_V,\cdots\rbrace$$
$$g^*(A)_U=g_U^{-1}A g_U+g_U^{-1}\dd(g_{U})$$
若$A’=g^*(A)$,则$A’$和$A$在物理上是等价的,商去规范变换空间可得到物理上不等价的联络空间
$$\mathscr{B}_P:=\mathscr{A}_P/\mathscr{G}_P$$
Yang-Mills理论
考虑G-主丛或其关联向量丛上的联络$A$和曲率$F$,记底空间维数$d=\dim M\ge 2$,则经典杨-米尔斯作用量可写为
$$\begin{aligned}
S_{YM}[A]&=\frac{1}{2g_{YM}^2}\int_M\Tr{F\wedge *F}\\
&=\frac{1}{2g^2_{YM}}\int_M\Tr({F_{\mu\nu}F^{\mu\nu}})\sqrt{g}\;\text{d}^d x
\end{aligned}$$
在平直时空中$\sqrt{g}=1$,考虑$G=SU(N)$,
选择李代数$\mathfrak{su}(N)$在$U$上的一组基$\displaystyle\Tr(T_aT_b)=\frac{1}{2}\delta_{ab}$,$F_{\mu\nu}=F_{\mu\nu}^aT_a$
$$S_{YM}[A]=\frac{1}{4g^2_{YM}}\int_MF_{\mu\nu}^aF^{b,\mu\nu}\delta_{ab}\;\text{d}^d x$$
$$F_{\mu\nu}^a=\partial_\mu A_\nu^a-\partial_\nu A_\mu^a+f_{bc}^{\;\;a} A_\mu^b A_\nu^c$$
因此杨-米尔斯理论是麦克斯韦理论的自然非阿贝尔推广,
由 $F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_\mu+[A_\mu,A_\nu]$ ,对$A_\nu$进行变分$A_\nu \mapsto A_\nu +\delta a_\nu$
$$\delta F_{\mu\nu}=\partial_\mu\delta a_\nu+[A_\mu,\delta a_\nu]$$
再对杨-米尔斯作用量变分
$$\begin{aligned}
\delta S_{YM}[A]&=\frac{1}{2g^2_{YM}}\int\Tr({\delta F_{\mu\nu},F^{\mu\nu}})\;\text{d}^d x\\
&=\frac{1}{2g^2_{YM}}\int\Tr({\nabla_\mu\delta a_\nu,F^{\mu\nu}})\;\text{d}^d x=0
\end{aligned}$$
可得Yang-Mills方程
$$\nabla^\mu F_{\mu\nu}:=\partial^\mu F_{\mu\nu}+[A^\mu,F_{\mu\nu}]=0$$
无指标形式为
$$\delta_A F=*\text{d}_A*F=*(\text{d}+A)*F=0$$
比安基恒等式在局部坐标下可表示为
$$\nabla_\mu F_{\nu\lambda}+\nabla_\nu F_{\lambda\mu}+\nabla_\lambda F_{\mu\nu}$$
与麦克斯韦方程组不同,这是$A$的非线性偏微分方程,叠加原理不再成立
杨-米尔斯路径积分可表示为
$$Z_{YM}=\int_{\mathscr{A}/\mathscr{G}}DA\exp(-iS_{YM}[A])$$
From Satoshi Nawata’s Differential Geometry and Topology in Physics: Spring-2023