Friedmann–Robertson–Walker度规
宇宙学原理 宇宙是均匀且各向同性的
唯一与宇宙学原理相容的背景是弗里德曼-罗伯逊-沃尔克度规,其线元为
$$\dd s^2=-c^2\dd t^2+a^2\left(\frac{\dd r^2}{1-kr^2}+r^2\dd \theta^2+r^2\sin^2\theta^2\dd\phi^2\right)$$
$a=a(t)$为标度因子,$k$为常数,可通过调节径向坐标使其取$-1,0,1$,对应三种情况
$k=1$,闭合宇宙;$k=0$,平坦宇宙;$k=-1$,开放宇宙
计算可得曲率标量 $R=\displaystyle 6\frac{kc^2+\dot{a}^2+\ddot{a}a}{a^2c^2}$,$k=0,\dot{a}=0$ 对应闵可夫斯基时空
克莱舒曼标量 $\mathscr{H}=\displaystyle\frac{k^2c^4+2kc^2\dot{a}^2+\dot{a}^4+\ddot{a}^2a^2}{a^4c^2}$,$a=0$ 为大爆炸
对于拓扑平凡宇宙,$k=0$ 时其体积有限 $V=\displaystyle\int_V g^{3/2}\text{d}^3 x=\pi^2 a^3$
Friedmann 方程组
假设宇宙物质由理想流体能动张量$T^{\mu\nu}=\displaystyle(\rho+P)\frac{u^\mu u^\nu}{c^2}+Pg^{\mu\nu}$描述,对于流体静止系,四维速度$u^\mu=(c,0,0,0)$
爱因斯坦方程 $tt$ 分量给出 第一弗里德曼方程,记$H=\displaystyle\frac{\dot{a}}{a}$ 为Hubble参数
$$H^2=\frac{8\pi G_N}{3c^2}\rho-\frac{kc^2}{a^2}$$
其他分量 给出第二弗里德曼方程
$$\frac{\ddot{a}}{a}=-\frac{4\pi G_N}{3c^2}(\rho +P)$$
能动张量协变性给出 $\displaystyle\dot{\rho}=-3H(\rho+P)$,但并不独立于以上两个方程
引入物态方程 $P=w\rho $,对尘埃$w=0$,辐射$w=\displaystyle-\frac{1}{3}$,真空$w=-1$
定义临界密度为平坦宇宙能量密度 $\rho_c=\displaystyle\frac{3H_0^2c^2}{8\pi G_N}$,哈勃常数目前测量值为$H_0=100h_0\displaystyle\frac{\text{km}}{\text{s}\cdot\text{Mpc}}$,$h_0\approx 0.7$
宇宙学模型
结合能动张量协变性和物态方程可得能量密度$\rho\propto \displaystyle a^{-3(1+w)}$
对尘埃$\rho\propto \displaystyle\frac{1}{a^3}$,对辐射 $\rho\propto \displaystyle\frac{1}{a^4}$,对真空 $\rho$ 为常数
代入第一弗里德曼方程,忽略$\displaystyle\frac{kc^2}{a^2}$ 项可得 $a\propto t^{\alpha}$,$\alpha=\displaystyle\frac{2}{3(1+w)}$
爱因斯坦宇宙
对于一般物质 $\rho+3P>0$,故弗里德曼方程隐含$\ddot{a}<0$,宇宙是不稳定的,爱因斯坦引入宇宙学常数$\varLambda$修正爱因斯坦场方程,弗里德曼方程成为
$$H^2=\frac{8\pi G_N}{3c^2}\rho+\frac{\Lambda c^2}{3}-\frac{kc^2}{a^2}$$
$$\frac{\ddot{a}}{a}=-\frac{4\pi G_N}{3c^2}(\rho +P)+\frac{\Lambda c^2}{3}$$
要求$\dot{a},\ddot{a}=0$,可解得$\rho=\displaystyle\frac{\Lambda c^4}{4\pi G_N}$,$a=\displaystyle\frac{1}{\sqrt{\Lambda}}$,$k=1$
然而爱因斯坦宇宙也是不稳定的,微小扰动会使其永远坍缩或膨胀,1929年哈勃发现宇宙膨胀后宇宙学常数暂时从爱因斯坦方程中被移除
物质主导的宇宙
令 $\rho=C_1/a^3$,第一弗里德曼方程成为$\displaystyle\dot{a}^2=\displaystyle\frac{8\pi G_N}{3c^2}\frac{C_1}{a}-kc^2$
引入 $\displaystyle\frac{\dd\eta}{\dd t}=\frac{1}{a}$,$’$代表对$\eta$求导,则$\displaystyle a’^2=\displaystyle\frac{8\pi G_N}{3c^2}C_1 a-kc^2a^2$,
根据初始条件$a(0)=0$,引入$A=\displaystyle\frac{1}{|k|c^2}$,解得
闭合宇宙
$$a=\frac{4\pi G_N}{3c^2}C_1A\left(1-\cos\frac{\eta}{\sqrt{A}}\right)\quad t=\frac{4\pi G_N}{3c^2}C_1A\left(\eta-\sqrt{A}\sin\frac{\eta}{\sqrt{A}}\right)$$
平坦宇宙
$$a=\frac{2\pi G_N}{3c^2}C_1\eta^2\quad t=\frac{2\pi G_N}{9c^2}C_1\eta^3$$
开放宇宙
$$a=\frac{4\pi G_N}{3c^2}C_1A\left(\cosh\frac{\eta}{\sqrt{A}}-1\right)\quad t=\frac{4\pi G_N}{3c^2}C_1A\left(\sqrt{A}\sinh\frac{\eta}{\sqrt{A}}-\eta\right)$$
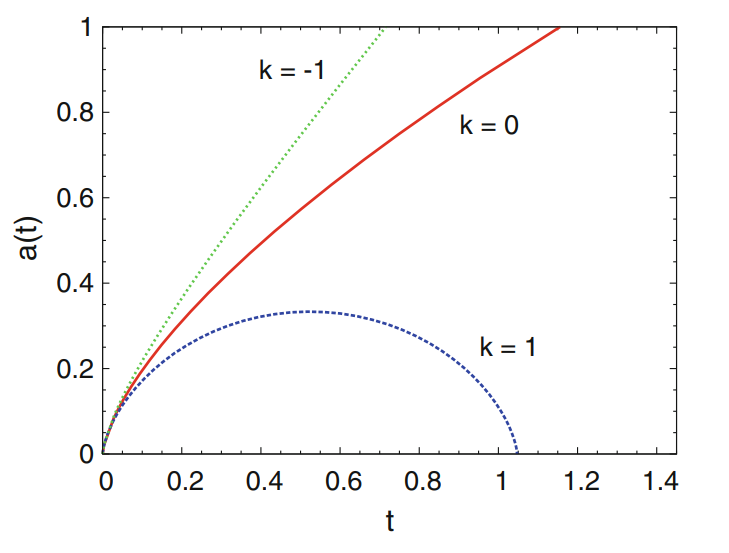
辐射主导的宇宙
令 $\rho=C_2/a^4$,第一弗里德曼方程成为$\displaystyle\dot{a}^2=\displaystyle\frac{8\pi G_N}{3c^2}\frac{C_2}{a^2}-kc^2$,可解得
$$a=\left[\sqrt{\frac{32\pi G_NC_2}{3c^2}}t-kc^2t^2\right]^{1/2}$$
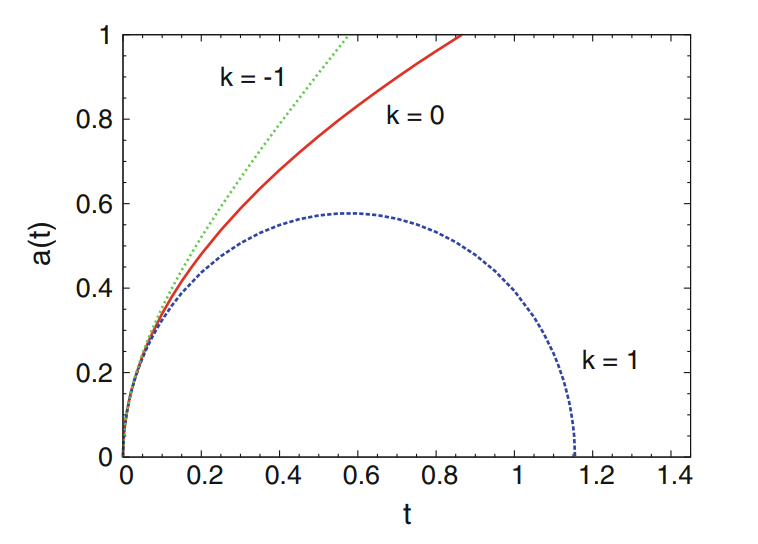
真空主导的宇宙
$\rho=P=0$,考虑宇宙学常数 $H^2=\displaystyle\frac{\Lambda c^2}{3}-\frac{kc^2}{a^2}$,$\displaystyle\frac{\ddot{a}}{a}=\displaystyle\frac{\Lambda c^2}{3}$
对于$\Lambda>0$,无论$k$取何值宇宙都将膨胀,不存在大爆炸
闭合宇宙
$$a=\sqrt{\frac{3}{\Lambda}}\cosh\left(\sqrt{\frac{\Lambda}{3}}ct\right)$$
平坦宇宙
$$a=a(0)\exp\left(\sqrt{\frac{\Lambda}{3}}ct\right)$$
开放宇宙
$$a=\sqrt{\frac{-3}{\Lambda}}\sinh\left(\sqrt{\frac{\Lambda}{3}}ct\right)$$
对于$\Lambda<0$,仅存在坍缩开放宇宙
$$$$
$$a=\sqrt{\frac{-3}{\Lambda}}\cos\left(\sqrt{-\frac{\Lambda}{3}}ct\right)$$
对于$\Lambda=0$,仅存在平坦闵可夫斯基时空
Friedmann–Robertson–Walker度规的性质
宇宙学红移
拉格朗日量$L=\displaystyle\frac{1}{2}g_{\mu\nu}x’^\mu x’^\nu$,$’$表示对固有时求导,由于度规与$t$有关,故粒子能量不是运动常数
对光子有 $g_{\mu\nu}x’^\mu x’^\nu=0$,考虑径向运动,则
$$c^2t’^2-a^2\frac{r’^2}{1-kr^2}=0$$
拉格朗日方程
$$t’’+\frac{a\dot{a}}{c^2}\frac{r’^2}{1-kr^2}=0$$
联立可得 $t’’=-\displaystyle\frac{a’}{a}t’$,$t’$ 正比于光子能量,故$E\propto\displaystyle\frac{1}{a}$,故宇宙膨胀会引起红移,这与$\rho\propto \displaystyle \frac{1}{a^4}$ 相符
粒子视界
位于$t$时刻的粒子视界为从大爆炸时刻至时间$t$,一个光子所传播的距离,考虑平坦宇宙
$$r=\displaystyle\int \text{d}r=c\int\frac{\dd t}{a}=\displaystyle\frac{ct}{a(1-\alpha)}$$
粒子视界随时间线性增长,而标度因子$a\propto t^{\alpha}$,对于物质和辐射主导的宇宙,$\alpha=\displaystyle\frac{2}{3(1+w)}<1$,随着时间推移,宇宙中越来越多的区域变得因果连通