球对称时空

线元$\dd s^2=-f(t,r)c^2\dd t^2+h(t,r)\dd t\dd r+g(t,r)(\dd r^2+r^2\dd\theta^2+r^2\sin^2\theta\dd\phi^2)$

关于$\theta,\phi$不变，故$g_{t\theta},g_{t\phi}=0$，变换坐标$t\to \tilde{t},r\to\tilde{r}$使得$\tilde{r}^2=g(t,r)r^2,g_{\tilde{t} \tilde{r}}=0$

坐标$\tilde{r}$几何意义为面积为$4\pi \tilde{r}^2$的球面径向坐标值，但并不描述至$\tilde{r}=0$的真实距离，度规简化为

$$\dd s^2=-fc^2\dd t^2+g\dd r^2+r^2(\dd\theta^2+\sin^2\theta\dd\phi^2)$$

有限扩张物质分布时空渐近平直，$\displaystyle\lim_{r \to\infty}f,\lim_{r \to\infty}g=1$

Birkhoff定理

伯克霍夫定理 真空中爱因斯坦方程唯一的球对称解为史瓦西度规

$$\dd s^2=-\left(1-\displaystyle\frac{2G_NM}{c^2r}\right)c^2\dd t^2+\frac{\dd r^2}{\displaystyle\left(1-\displaystyle\frac{2G_NM}{c^2r}\right)}+r^2(\dd\theta^2+\sin^2\theta\dd\phi^2)$$

Schwarzschild度规

史瓦西半径 $r_s=\displaystyle\frac{2G_NM}{c^2}$

固有时$\dd\tau=\displaystyle\sqrt{1-\frac{r_S}{r}}\dd t$，固有距离$\displaystyle\dd\rho=\frac{\dd r}{\displaystyle\sqrt{1-\frac{r_S}{r}}}$，$\Delta\rho=r_2-r_1+\displaystyle\frac{r_S}{2}\ln{\frac{r_2}{r_1}}$

史瓦西坐标与位于无穷远的观测者的坐标相契合

在史瓦西度规中的运动

简单起见，令$k=0,1$ 分别为无质量和有质量粒子的质量，系统拉格朗日量为

$$L=\frac{1}{2}g_{\mu\nu}\dot{x}^\mu\dot{x}^\nu$$

考虑赤道运动 $\theta=\displaystyle\frac{\pi}{2}$，$L=\displaystyle\frac{1}{2}(-fc^2\dot{t}^2+g\dot{r}^2+r^2\dot{\phi}^2)$，$f=1/g=1-\displaystyle\frac{r_S}{r}$

三个运动常数为无穷远处能量$E=fc^2\dot{t}$，角动量$L_z=r^2\dot{\phi}$，质量$kc^2=-2L$

将$E,L_z$ 代入$L$得

$$g\dot{r}^2+\frac{L_z^2}{r^2}-\frac{E^2}{c^2f}=-kc^2\tag{1}\label{eq1}$$

代入$f,g$ 得$\displaystyle\frac{1}{2}\dot{r}^2+\left(1-\frac{r_S}{r}\right)\frac{L_z^2}{2r^2}-\frac{1}{2}\frac{E}{c^2}=-\frac{1}{2}\left(1-\frac{r_S}{r}\right)kc^2$

令$V_\text{eff}=\displaystyle-k\frac{G_NM}{r}+\left(1-\frac{r_S}{r}\right)\frac{L_z^2}{2r^2}$

$$\displaystyle\frac{1}{2}\dot{r}^2=\frac{E^2-kc^4}{2c^2}-V_\text{eff}$$

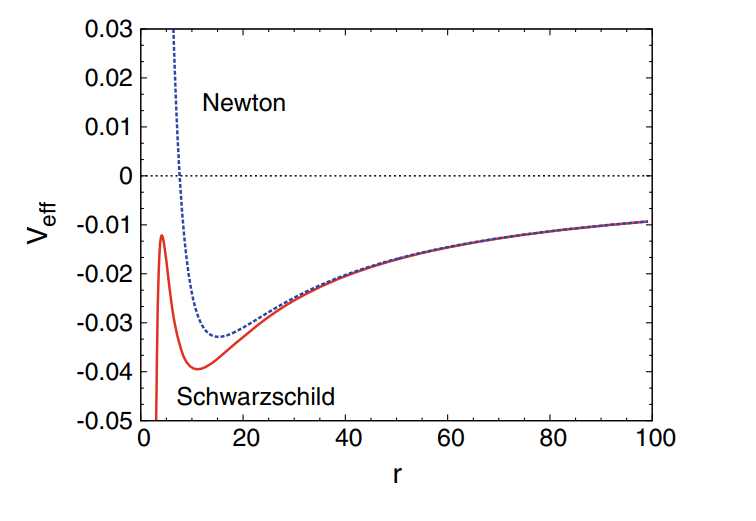
对牛顿有效势有 $r^{-3}$ 修正，带来在半径很小处的明显差异

现在推导开普勒定律 $\dot{r}=\displaystyle\frac{\dd r}{\dd\phi}\dot{\phi}$，代入$E,L_z$ ，令$u=\displaystyle\frac{1}{r},u’=\frac{\dd u}{\dd \phi}$

$$u’^2-k\frac{2G_NM}{L_z^2}u+u^2-\frac{2G_NM}{c^2}u^3=\frac{E^2-kc^4}{c^2L_z^2}$$

求导得轨道方程

$$u’’-k\frac{G_NM}{L_z^2}+\left(1-\frac{3r_S}{2r}\right)u=0$$

史瓦西黑洞

$r=r_S$ 处 $g^{rr}=0$，为黑洞视界，由$\eqref{eq1}$ ，径向运动的角速度为零有质量粒子

$$\dd t=\frac{1}{c}\frac{E}{1-\displaystyle\frac{r_S}{r}}\frac{\dd r}{\sqrt{E^2-c^4+\displaystyle\frac{r_Sc^4}{r}}}$$

在视界处$\Delta t$ 发散，但$\Delta\tau$ 有限，说明有质量粒子可以穿过视界进入黑洞，而在远处的观测者却永远也无法看到粒子穿过视界

引入Kreshmann标量，$\mathscr{H}=R^{\mu\nu\rho\sigma}R_{\mu\nu\rho\sigma}$，其敛散性可以区别时空的奇性是否本质

对于史瓦西黑洞，$\mathscr{H}=\displaystyle\frac{12r_S^2}{r^6}$，在$r_S$ 处并不发散，因此度规在此处的奇性可以通过坐标变换消除

引入 Lemaître坐标

$\displaystyle\dd T=\dd t+\frac{1}{c}\left(\frac{r_S}{r}\right)^{1/2}\left(1-\frac{r_S}{r}\right)^{-1}$

$\displaystyle\dd R=\dd t+\frac{1}{c}\left(\frac{r}{r_S}\right)^{1/2}\left(1-\frac{r_S}{r}\right)^{-1}$

$r=(r_S)^{1/3}\left[\displaystyle\frac{3}{2}(R-cT)\right]^{2/3}$

史瓦西线元变为

$$\dd s^2=-c^2\dd T^2+\frac{r_S}{r}\dd R^2+r^2(\dd\theta^2 +\sin^2\theta\dd\phi^2)$$

在勒梅特坐标下，视界处的奇性得以消除，黑洞内部除奇点外的时空也能被良好描述

引入 Kruskal-Szekeres 坐标，

$$\tilde{t}\left\lbrace\begin{matrix}
\displaystyle\left(\frac{r}{r_S}-1\right)^{1/2}e^{r/(2r_S)}\sinh\left(\frac{ct}{2r_S}\right)& r>r_S\\
\displaystyle\left(1-\frac{r}{r_S}\right)^{1/2}e^{r/(2r_S)}\cosh\left(\frac{ct}{2r_S}\right)& 0<r<r_S
\end{matrix}\right.$$

$$\tilde{r}\left\lbrace\begin{matrix}
\displaystyle\left(\frac{r}{r_S}-1\right)^{1/2}e^{r/(2r_S)}\cosh\left(\frac{ct}{2r_S}\right)& r>r_S\\
\displaystyle\left(1-\frac{r}{r_S}\right)^{1/2}e^{r/(2r_S)}\sinh\left(\frac{ct}{2r_S}\right)& 0<r<r_S
\end{matrix}\right.$$

在克鲁斯卡尔-塞凯赖什坐标下，得到史瓦西时空的最大解析延拓，线元成为

$$\dd s^2=\frac{4r_S^2}{r}e^{-r/r_S}(-\text{d} \tilde{t}^2+\text{d}\tilde{r}^2)+r^2(\dd\theta^2+\sin^2\theta\dd\phi^2)$$

Penrose Diagram

闵可夫斯基时空

对球坐标进行共形变换

$$t=\displaystyle\frac{1}{2}\left(\tan\frac{T+R}{2}+\tan\frac{T-R}{2}\right)$$

$$r=\displaystyle\frac{1}{2}\left(\tan\frac{T+R}{2}-\tan\frac{T-R}{2}\right)$$

令$c=1$，平直时空线元成为

$$\dd s^2=\left(4\cos^2\frac{T+R}{2}\cos^2\frac{T-R}{2}\right)^2(-\dd T^2+\dd R^2)+r^2(\dd\theta^2+\sin^2\theta\dd\phi^2)$$

使用记号

类时未来无限 $i^+$
类时过去无限 $i^-$
类空无限 $i^0$
类光未来无限 $\mathscr{T}^+$
类光过去无限 $\mathscr{T}^-$

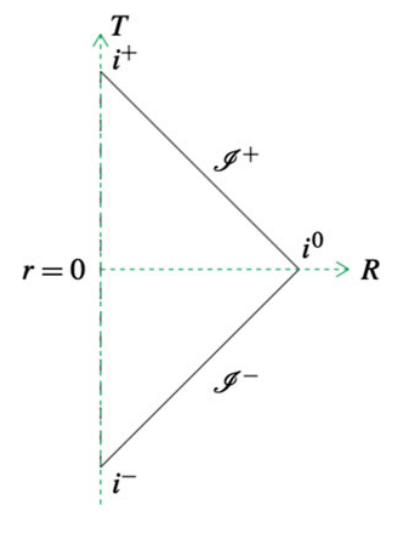
画出闵可夫斯基时空彭罗斯图，其上每点对应一个二维球面，$45\degree$ 直线代表类光测地线

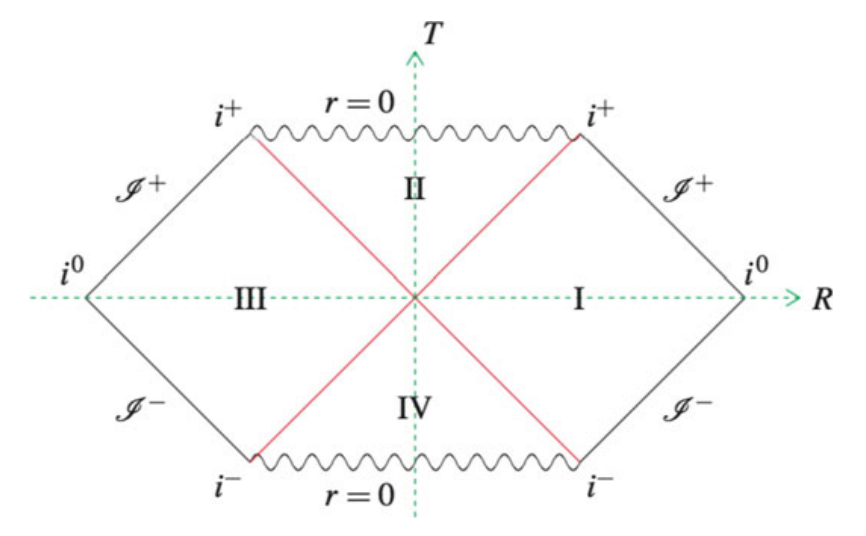
史瓦西时空

对克鲁斯卡尔-塞凯赖什坐标下的史瓦西时空进行与闵可夫斯基时空相同的坐标变换，得到线元

$$\dd s^2=\frac{32G_N^3M^3}{r}e^{-r/(2G_NM)}\left(4\cos^2\frac{T+R}{2}\cos^2\frac{T-R}{2}\right)^2(-\dd T^2+\dd R^2)+r^2(\dd\theta^2+\sin^2\theta\dd\phi^2)$$

史瓦西时空的最大延拓彭罗斯图如下，