模形式
定义1$\quad$令$L$为$\mathbb{C}$中所有平行四边形格点阵$\Lambda$的集合,若映射$F:L\to\mathbb{C}$为$-k\le 0$阶齐次方程且在$L$和$\infty$上全纯,则称$F$为权为$k$的模形式
对每个$\Lambda$,取其基本周期对$\langle \omega_1,\omega_2\rangle$ 使得 $\Im\displaystyle\frac{\omega_1}{\omega_2}>0$,对应$\mathbb{H}$中一点$z=\displaystyle\frac{\omega_1}{\omega_2}$
由模函数齐次条件,$F( \omega_1\mathbb{Z}+\omega_2\mathbb{Z})=\omega_2^{-k}F(z\mathbb{Z}+\mathbb{Z})$,定义$f(z)=F(z\mathbb{Z}+\mathbb{Z})$
由于对$z$作变换 $\gamma\in \text{SL}_2(\mathbb{Z}):z\mapsto \displaystyle\frac{az+b}{cz+d}$ 后格点不变
$$f(\gamma z)=(cz+d)^kF((az+b)\mathbb{Z}+(cz+d)\mathbb{Z})=F(z\mathbb{Z}+\mathbb{Z})$$
可以得到模形式的等价定义
定义2$\quad$若$f:\mathbb{H}\to\mathbb{C}$在$\mathbb{H}$和$\infty$上全纯,且满足以下条件,则称$f$为权为$k$的模形式
$$f(\gamma z)=(cz+d)^kf(z)$$
引入$k$权算子$[\gamma]_k$,其中自守因子 $j_\gamma(z)=cz+d$,
$$f[\gamma]_k(z)=j_\gamma(z)^{-k}f(\gamma z)$$
算子具有以下性质
$1.\quad$$j_{\gamma_1\gamma_2}(z)=j_{\gamma_1}(\gamma_2 z)j_{\gamma_2}(z)$
$2.\quad$$(\gamma_1\gamma_2 )z=\gamma_1(\gamma_2 z)$
$3.\quad$$f[\gamma_1\gamma_2]_k= (f[\gamma_1]_k) [\gamma_2]_k$
$4.\quad$$\Im\;(\gamma z)=\displaystyle\frac{\Im\;z}{|j_\gamma(z)|^2}$
现在 $\text{SL}_2(\mathbb{Z})$ 下的弱模条件可简记为
$$f[\gamma]_k=f\qquad\forall{\gamma\in \text{SL}_2(\mathbb{Z})}$$
若$f(\infty)=0$,则称$f$为尖点形式;若将全纯改为亚纯,则退化为在$\text{SL}_2(\mathbb{Z})$下自守的模函数的定义,以下提及模函数均默认其在$\text{SL}_2(\mathbb{Z})$下自守
记所有权为$k$的模形式的集合为$\mathcal{M}_k(\text{SL}_2(\mathbb{Z}))$,尖点形式的集合为$\mathcal{S}_k(\text{SL}_2(\mathbb{Z}))$,简记为$\mathcal{M}_k$和$\mathcal{S}_k$
由定义知不同权模形式线性独立,同权模形式之比为模函数,$\mathcal{M}_{k_1}\mathcal{M}_{k_2}\subset\mathcal{M}_{k_1+k_2}$
取$\gamma=-I_2$,$f(z)=(-1)^kf(z)$,故除零以外不存在权为奇数的模形式
取$\gamma=T=\displaystyle\begin{pmatrix}
1&1\\0&1
\end{pmatrix}$,$f(z+1)=f(z)$,模形式周期为$1$
取$\gamma=S=\displaystyle\begin{pmatrix}0&1\\-1&0
\end{pmatrix}$,$f(-1/z)=(-z)^kf(z)$
由于 $\text{SL}_2(\mathbb{Z})$ 可由$T,S$ 生成,故满足如下两个模变换规律即为模形式
$$f(z+1)=f(z)$$
$$f(-1/z)=(-z)^kf(z)$$
$k\ge 3$ 时,$G_k(\Lambda)=\displaystyle\sum_{\omega\in\Lambda^*}\frac{1}{\omega^k}$ 为模形式,但不是尖点形式
利用黎曼$\zeta$函数取值 $\zeta(4)=\displaystyle\frac{\pi^4}{90},\zeta(6)=\frac{\pi^6}{945}$
可知 $\Delta=g_2^3-27g_3^2=(60G_4)^3-27(140G_6)^2$ 为12权尖点形式
$\infty$为j-不变量 $j=\displaystyle\frac{1728g_2^3}{\Delta}$ 单极点,因此$j$为0权模函数,但不是模形式
级数展开
由于模形式周期为$1$,故可用 $q=e^{i2\pi z}$ 展开
$$f(z)=\sum_{n=0}^\infty a_n q^n$$
利用 $\sin{\pi z}=\pi z\displaystyle\prod_{m=1}^\infty\left(1-\frac{z^2}{m^2}\right)$,两边取对数后求二阶导可得
引理1$\quad$$k\ge 2$,$z\in\mathbb{H}$
$$\sum_{m\in\mathbb{Z}}\frac{1}{(z+m)^k}=\frac{(-2\pi i)^k}{(k-1)!}\sum_{m=1}^\infty m^{k-1}q^{m}$$
由引理可得 $G_k(z)=G_k(z\mathbb{Z}+\mathbb{Z})$ 展开式,默认$k\ge 4$且为偶数
引入除数函数 $\sigma_s(n)=\displaystyle\sum_{d|n}d^s$,其满足 $\sigma_s(mn)=\sigma_s(m)\sigma_s(n)$
$$G_k(z)=2\zeta(k)+2\frac{(2\pi i)^k}{(k-1)!}\sum_{n=1}\sigma_{k-1}(n)q^n$$
尖点形式 $\Delta(z)$ 可写为
$$\Delta(z)=(12\pi)^{12}\sum_{n=1}^\infty\tau(n)q^n$$
$\tau$称为Ramanujan $\tau$ 函数,计算发现 $\tau(n)$ 的前几个值均为整数
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| $\tau(n)$ | 1 | -24 | 252 | -1472 | 4830 | -6048 | -16744 | 84480 |
引入Dedekind $\eta$ 函数
$$\eta(z)=q^{1/24}\prod_{n=1}^\infty(1-q^n)$$
计算对数导数得到变换规律 $\eta(-1/z)=\sqrt{-iz}\;\eta(z)$,可知 $\eta^{24}(z)$ 为12权尖点形式
由下一节可知 $\dim_\mathbb{C}{\mathcal{S}_{12}}=1$,因此 $\Delta$ 与 $\eta^{24}$ 线性相关
比较系数可得以下 $\Delta$ 无穷乘积,由此说明 $\tau(n)\in\mathbb{Z}$
$$\Delta(z)=(2\pi)^{12}q\prod_{n=1}^\infty(1-q^n)^{24}$$
Ramanujan猜想$\quad$
$1.\quad$若$m,n$互素,则$\tau(mn)=\tau(m)\tau(n)$
$2.\quad$对素数$p$,$\tau(p^{r+1})=\tau(p)\tau(p^r)-p^{11}\tau(p^{r-1})$
$3.\quad$对素数$p$,$|\tau(p)|\le 2p^{11/2}$
维度公式
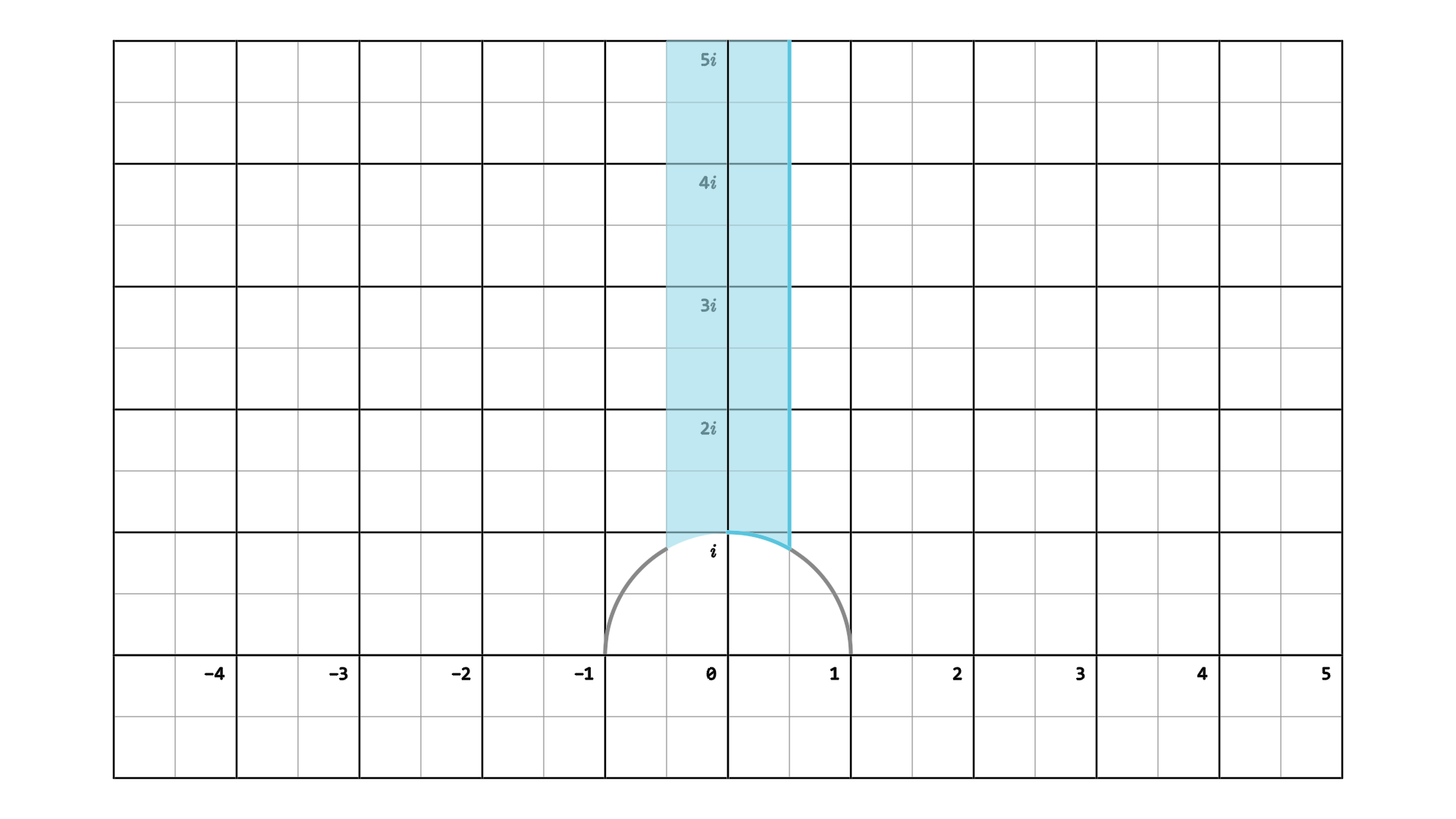
设$f$为模函数,将$\displaystyle\frac{f’}{f}$在如图所示基本域$\mathcal{F}$边界上积分得
定理1$\quad$对非零$k$权模函数 $f:\mathbb{H}\to\mathbb{C}$,记$\text{ord}_z$为$f$在$z$处阶数,零点为正,极点为负
$$\text{ord}_\infty+\frac{1}{2}\text{ord}_i+\frac{1}{3}\text{ord}_{e^{\pi i/3}}+\sum_{z\in\mathcal{F}\backslash\{i,e^{\pi i/3}\}}\text{ord}_z=\frac{k}{12}$$
定理2
$$\dim_\mathbb{C}\mathcal{M}_k=\left\lbrace\begin{array}{l}\lfloor k/12\rfloor & k= 2\;(\text{mod}\; 12)\\\lfloor k/12\rfloor+1 & k\neq 2\;(\text{mod}\; 12)\end{array}\right.$$
$$\dim_\mathbb{C}\mathcal{S}_k=\dim_\mathbb{C}\mathcal{M}_k-1$$
由维度公式知非零模形式的权数 $k\ge 4$
推论1$\quad$$G_4$和$G_6$代数独立,且可以生成所有模形式
$$\bigoplus_{k=1}^\infty\mathcal{M}_k=\mathbb{C}[G_4,G_6]$$
椭圆曲线
由Weirstrass椭圆函数微分方程
$$\wp’^2(z)=4\wp^3(z)-g_2\wp(z)-g_3$$
每个格点阵 $\Lambda$ 对应如下复椭圆曲线 $E_\Lambda=\overline{V(f)}$
$$f(x,y)=4x^3-g_2x-g_3-y^2$$
$E_\Lambda$ 上点具有形式 $P(z)=(\wp(z),\wp’(z))$,其上无穷远点记为 $O=(\wp(0),\wp’(0))$
由于 $z+\Lambda\in \mathbb{C}/\Lambda$ 与 $P(z)$ 之间存在双射,故可定义椭圆曲线上点的加法
$$P(z_1)+P(z_2)=P(z_1+z_2)$$
可知无穷远点 $O$ 在此加法下的地位相当于零
联立 $E_\Lambda$ 与直线方程,构造椭圆函数 $l(z)=a\wp(z)+b\wp’(z)+c$
若 $b \neq 0$ ,由于原点为 $l(z)$ 三阶极点,故 $l(z)$ 三个零点满足 $z_1+z_2+z_3\in\Lambda$
若 $b=0$ ,原点为 $l(z)$ 二阶极点,$l(z)$ 两个零点满足 $z_1+z_2\in\Lambda$
在 $b=0$ 情况下,将 $O$ 视为 $l$ 与 $E_\Lambda$ 的第三个交点,于是 $l$ 与 $E_\Lambda$ 的三个交点满足
$$P_1+P_2+P_3=O$$
由此可知椭圆曲线上两点相加得到其连线与椭圆曲线的另一个交点关于$x$轴的对称点
利用$j(z)$建立的基本域与$\mathbb{C}$之间的双射,可知
定理3$\quad$对任意复椭圆曲线$y^2=4x^3-a_2x-a_3$,$a_2^3-27a_3^2$,
均存在$\Lambda$,使得$g_2(\Lambda)=a_2,g_3(\Lambda)=a_3$
同余子群
引理2$\quad$若$\Gamma$为$\text{SL}_2(\mathbb{Z})$的有限指数子群,则
$1.\quad$$\text{SL}_2(\mathbb{Z})$ 对 $\overline{\mathbb{Q}}$ 的群作用可迁
$2.\quad$$\text{SL}_2(\mathbb{Z})_x$ 非平凡(含抛物变换)当且仅当 $x\in\overline{\mathbb{Q}}$
$3.\quad$对 $x\in\overline{\mathbb{Q}}$,$\Gamma_x$ 为抛物变换生成的循环群
$4.\quad$$\Gamma$ 作用于 $\overline{\mathbb{Q}}$ 得到的轨道数目有限
$\Gamma$-轨道称为尖点,称属于同一轨道的元素$\Gamma$-等价,$\Gamma(1)=\text{SL}_2(\mathbb{Z})$ 只有一个尖点
定义3$\quad$若$f:\mathbb{H}\to\mathbb{C}$ 在 $\mathbb{H}$ 和 $\Gamma$-尖点上全纯,且满足 $\Gamma$ 下的弱模条件,则称$f$为 $\Gamma$ 下权为$k$的模形式
$$f[\gamma]_k=f\qquad \forall{\gamma}\in \Gamma$$
记 $\text{SL}_2(\mathbb{Z})$ 的模 $n$ 同余主子群为 $\Gamma(n)\equiv I_2(\text{mod}\; n)$
记 $\text{SL}_2(\mathbb{Z})$ 两个常用模 $n$ 同余子群 为
$\Gamma_0(n)\equiv\displaystyle\begin{pmatrix}
* & *\\ 0 &*
\end{pmatrix}(\text{mod}\; n),\Gamma_1(n)\equiv\displaystyle\begin{pmatrix}
1 & *\\ 0 &1
\end{pmatrix}(\text{mod}\; n)$
记$p$为素数,利用 Euler totient 函数 $\phi(n)=\displaystyle n\prod_{p|n}(1-p^{-1})$ 与商关系
$\#\text{GL}_2(\mathbb{Z}_p)=(p^2-1)(p^2-p)$,$[\text{GL}_2(\mathbb{Z}_p):\text{SL}_2(\mathbb{Z}_p)]=p-1$
$[\mathbb{Z}_{p^{m+1}}:\mathbb{Z}_{p^m}]=p$,$\mathbb{Z}_n=\displaystyle\bigoplus_{i}\mathbb{Z}_{p_i^{m_i}}\quad n=\prod_{i}p_i^{m_i}$
$[\Gamma(1):\Gamma(n)]=\# \text{SL}_2(\mathbb{Z}_n)$,$[\Gamma(n):\Gamma_1(n)]=n$,$[\Gamma_0(n):\Gamma_1(n)]=\phi(n)$
可得以下公式
$$[\Gamma(1):\Gamma(n)]=n^3\prod_{p|n}(1-p^{-2})$$
$$[\Gamma(1):\Gamma_1(n)]=n^2\prod_{p|n}(1-p^{-2})$$
$$[\Gamma(1):\Gamma_0(n)]=n\prod_{p|n}(1+p^{-1})$$
引理3$\quad$ $\overline{\mathbb{Q}}$ 中两个最简分数 $\displaystyle\frac{a}{b},\frac{c}{d}$ 属于相同 $\Gamma(n)$-尖点的充要条件为
$$\begin{pmatrix}a\\b\end{pmatrix}\equiv \pm \begin{pmatrix}c\\d\end{pmatrix} \quad(\text{mod}\; n)$$
引理4$\quad$ 若 $(a,b)\in\mathbb{Z}^2$,$(\bar{a},\bar{b})\in\mathbb{Z}_n^2$ 为其模$n$等价对,则以下三个条件等价
$1.\quad$$(a,b)$ 存在互素模$n$等价对
$2.\quad$$\gcd(a,b,n)=1$
$3.\quad$$$
由引理可得 $\Gamma(n)$-尖点的数目 $h_n$
$$h_n=\left\{\begin{array} & \displaystyle\frac{n^2}{2}\prod_{p|n}(1-p^{-2}) & n>2\\3 & n=2\end{array}\right.$$
Poincaré 级数
由 $G_k$ 定义标准 Eisenstein 级数 $E_k$,利用 $\zeta(k)=\displaystyle\prod_p\left(1-p^{-1}\right)^{-1}$
$$E_k(z):=\frac{G_k(z)}{2\zeta(k)}=\frac{1}{2}\sum_{\gcd(c,d)=1}\frac{1}{(cz+d)^k}$$
其用 $q=e^{i2\pi z}$ 展开如下,其中$B_k$为Bernoulli数,$\displaystyle\frac{t}{e^t-1}=\sum_{k=0}^\infty B_k\frac{t^k}{k!}$
$$E_k(z)=1-\frac{2k}{B_k}\sum_{n=1}^\infty\sigma_{k-1}(n)q^n$$
记 $\mathbb{Z}_{\text{pr}}^2=\{(c,d)\in\mathbb{Z}^2:\gcd(c,d)=1\}$,$\Gamma=\text{SL}_2(\mathbb{Z})$
无穷远点的稳定化子 $\Gamma_\infty=\left\langle\pm\begin{pmatrix}1&1\\0&1\end{pmatrix}\right\rangle$,其中元素第二行恒为 $\pm(0,1)$
由于对 $\mathbb{Z}_{\text{pr}}^2$ 中任意元素 $(c,d)$ ,均存在 $\gamma=\displaystyle \begin{pmatrix}a&b\\c&d\end{pmatrix} \in \Gamma$
故可定义如下映射,易知其为双射
$$\Gamma_\infty\backslash\Gamma\to \mathbb{Z}_{\text{pr}}^2/\pm\qquad\Gamma_\infty\gamma\mapsto (0,1)\gamma$$
默认$k$为偶数,因此Eisenstein级数可写为
$$E_k(z)=\sum_{\gamma\in \Gamma_\infty\backslash\Gamma}j_\gamma(z)^{-k}$$
定义4$\quad$若 $p:\mathbb{H}\to\mathbb{C}$ 全纯且周期为 $1$,则称如下级数为 Poincaré 级数
$$P(z)=\sum_{\gamma\in\Gamma_\infty\backslash\Gamma}j_\gamma(z)^{-k}p(\gamma z)$$
当 $p=q^m\quad m\ge 0$ 时,称其为第$m$个$k$权Poincaré 级数,记为 $P_{m,k}$
对同一个陪集中的 $\gamma_1,\gamma_2$,可以找出 $\gamma_0\in \Gamma_\infty$ ,使得 $\gamma_2=\gamma_0\gamma_1$
由 $j_{\gamma_0\gamma_1}(z)=j_{\gamma_0}(\gamma_1 z)j_{\gamma_1}(z)=\pm j_{\gamma_1}(z)$,$p(\gamma_0\gamma_1 z)= p(\gamma_1 z+m)=p(\gamma_1 z)$
可知Poincaré 级数独立于陪集中代表元的选取,因此是良定义的
利用 $j_\gamma(z)$ 的性质还可以证明 $P_{m,k}$ 为模形式
引理5$\quad$对$m\ge 1$,$P_{m,k}\in\mathcal{S}_k$
若 $\Gamma$ 为 $\text{SL}_2(\mathbb{Z})$ 同余子群,记其不等价尖点集合为 $\mathcal{C}_\Gamma$,取 $\mathfrak{a}\in \mathcal{C}_\Gamma$,$\sigma_\mathfrak{a}$ 为将 $\infty$ 映到$\mathfrak{a}$ 的变换矩阵
定义5$\quad$若 $p:\mathbb{H}\to\mathbb{C}$ 全纯且周期为 $1$,则称如下级数为$\Gamma$在$\mathfrak{a}$处的 Poincaré 级数
$$P_\mathfrak{a}(z)=\sum_{\gamma\in\Gamma_\mathfrak{a}\backslash\Gamma}j_{\sigma_\mathfrak{a}^{-1}\gamma}(z)^{-k}p(\sigma_\mathfrak{a}^{-1}\gamma z)$$
当 $p=q^m\quad m\ge 0$ 时,称其为$\Gamma$在$\mathfrak{a}$处的第$m$个Poincaré 级数,记为 $P_{\mathfrak{a},m}$,称 $E_{\mathfrak{a}}=P_{\mathfrak{a},0}$ 为 $\Gamma$在$\mathfrak{a}$处的Eisenstein 级数
易知以上定义的级数同样独立于陪集中代表元的选取
容易验证 $k\ge 3,m\ge 0$ 时,$P_{\mathfrak{a},m}$ 满足 $\Gamma$ 下的弱模条件,若其在 $\mathcal{C}_\Gamma$ 上全纯即可证明 $P_{\mathfrak{a},m}$ 为 $\Gamma$ 下的模形式
令$k\ge 4,m\ge 1$,将尖点形式 $P_{m,k}$ 用 $q=e^{i2\pi z}$ 展开
$$P_{m,k}(z)=\sum_{n=1}^\infty \hat{p}(m,n)q^n\qquad \hat{p}(m,n)=\int_0^1P_{m,k}(z)q^{-n}\dd x$$
引入经典 Kloosterman 和 $S(m,n;c)$
$$S(m,n;c)=\sum_{ad \equiv 1 (\text{mod}\;c)}\exp\left(2\pi i\times\frac{ma+nd}{c} \right)$$
$S(m,n;c)$ 满足如下性质
$1.\quad$$S(m,n;c)=S(n,m;c)$
$2.\quad$若 $\gcd(a,c)=1$,则 $S(am,n;c)=S(m,an;c)$
$3.\quad$$f[\gamma_1\gamma_2]_k= (f[\gamma_1]_k) [\gamma_2]_k$