正则量子化

自由实标量场的量子化

标量场满足以下对易关系

$$[\phi(\boldsymbol{x}),\pi(\boldsymbol{y})]=i\delta^3(\boldsymbol{x}-\boldsymbol{y})$$

$$[\phi(\boldsymbol{x}),\phi(\boldsymbol{y})]=0=[\pi(\boldsymbol{x}),\pi(\boldsymbol{y})]$$

对场进行Fourier变换，令 $E_\boldsymbol{p}=\sqrt{|\boldsymbol{p}|^2+m^2}$

$$\phi(\boldsymbol{x})=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{p}}}(a_\boldsymbol{p}e^{i\boldsymbol{p}\cdot\boldsymbol{x}}+a_\boldsymbol{p}^\dagger e^{-i\boldsymbol{p}\cdot\boldsymbol{x}})$$

$$\pi(\boldsymbol{x})=\int\frac{\text{d}^3 p}{(2\pi)^3}(-i)\sqrt{\frac{E_\boldsymbol{p}}{2}}(a_\boldsymbol{p}e^{i\boldsymbol{p}\cdot\boldsymbol{x}}-a_\boldsymbol{p}^\dagger e^{-i\boldsymbol{p}\cdot\boldsymbol{x}})$$

与谐振子类似，式中 $a_\boldsymbol{p}^\dagger,a_\boldsymbol{p}$ 即为产生湮灭算符

$$a_\boldsymbol{p}=\int\text{d}^3 x\; \left(\sqrt{\frac{E_\boldsymbol{p}}{2}}\phi(\boldsymbol{x})+\frac{i}{\sqrt{2E_\boldsymbol{p}}}\pi(\boldsymbol{x})\right)e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}$$

$$a_\boldsymbol{p}^\dagger=\int\text{d}^3 x\; \left(\sqrt{\frac{E_\boldsymbol{p}}{2}}\phi(\boldsymbol{x})-\frac{i}{\sqrt{2E_\boldsymbol{p}}}\pi(\boldsymbol{x})\right)e^{i\boldsymbol{p}\cdot\boldsymbol{x}}$$

$$[a_\boldsymbol{p},a_\boldsymbol{q}^\dagger]=(2\pi)^3\delta^3(\boldsymbol{p}-\boldsymbol{q})$$

$$[a_\boldsymbol{p},a_\boldsymbol{q}]=0=[a_\boldsymbol{p}^\dagger,a_\boldsymbol{q}^\dagger]$$

将自由标量场Hamiltonian用产生湮灭算符表示

$$\begin{aligned}H&=\int\text{d}^3x\;\left[\frac{1}{2}\pi^2+\frac{1}{2}(\nabla\phi)^2+\frac{1}{2}m^2\phi^2\right]\\&=\int\text{d}^3x\int\frac{\text{d}^3p\;\text{d}^3q}{(2\pi)^6}e^{i(\boldsymbol{p}+\boldsymbol{q})\cdot\boldsymbol{x}}\left[-\frac{\sqrt{E_\boldsymbol{p}E_\boldsymbol{q}}}{4}(a_\boldsymbol{p}-a_{\boldsymbol{-p}}^\dagger)(a_\boldsymbol{q}-a_{\boldsymbol{-q}}^\dagger)+\frac{-\boldsymbol{p}\cdot\boldsymbol{q}+m^2}{4\sqrt{E_\boldsymbol{p}E_\boldsymbol{q}}}(a_\boldsymbol{p}+a_{\boldsymbol{-p}}^\dagger)(a_\boldsymbol{q}+a_{\boldsymbol{-q}}^\dagger)\right]\\&=\int\frac{\text{d}^3 p}{(2\pi)^3}E_\boldsymbol{p}\left(a_\boldsymbol{p}^\dagger a_\boldsymbol{p}+\frac{1}{2}[a_\boldsymbol{p},a_\boldsymbol{p}^\dagger]\right)\end{aligned}$$

在无限的空间中积分导致Hamiltonian的发散，由于 $\displaystyle\int_{\mathbb{R}^3}\text{d}^3x\;e^{i\boldsymbol{p}\cdot\boldsymbol{x}}=(2\pi)^3\delta^3(\boldsymbol{p})$，式中发散项 $V_{\mathbb{R}^3}=(2\pi)^3\delta^3(0)$ 可视作 $\mathbb{R}^3$ 的体积，可自然将其舍弃

将算符 $O$ 中的产生算符全部移至湮灭算符的左侧，称为正规序，表示为 $:O:$

$$:H:\;=\int\frac{\text{d}^3 p}{(2\pi)^3}E_\boldsymbol{p}a_\boldsymbol{p}^\dagger a_\boldsymbol{p}$$

$$[H,a_\boldsymbol{p}^\dagger]=E_\boldsymbol{p}a_\boldsymbol{p}^\dagger\qquad [H,a_\boldsymbol{p}]=-E_\boldsymbol{p}a_\boldsymbol{p}$$

类似地，可将动量算符用产生湮灭算符表示，记真空态为 $\ket{0}$，对应舍弃发散项之后的能量 $E=0$，所有能量本征态可由产生算符作用于基态得到，通常将其归一化为以下形式，所有本征态构成Fock空间

$$\boldsymbol{P}=-\int\text{d}^3x\;\pi(\boldsymbol{x})\nabla\phi(\boldsymbol{x})=\int\frac{\text{d}^3 p}{(2\pi)^3}\,\boldsymbol{p}\,a_\boldsymbol{p}^\dagger a_\boldsymbol{p}$$

$$\ket{\boldsymbol{p}_1,\cdots,\boldsymbol{p}_n}=\sqrt{2E_{\boldsymbol{p}_1}\cdots2E_{\boldsymbol{p}_n}}\;a_{\boldsymbol{p}_1}^\dagger\cdots a_{\boldsymbol{p}_n}^\dagger\ket{0}\qquad E=\sum_{i=1}^n E_{\boldsymbol{p}_i}$$

Lorentz不变性

由于 $\delta^3(\boldsymbol{p}-\boldsymbol{q})$ 在boost作用下变为以下形式，故单粒子态内积在Lorentz变换下不变

$$\begin{aligned}\delta^3(\boldsymbol{p}’-\boldsymbol{q}’)&=\delta^3(\boldsymbol{p}-\boldsymbol{q})\frac{\dd p_1}{\dd p_1’}=\delta^3(\boldsymbol{p}-\boldsymbol{q})\gamma\left(1+v\frac{\dd E_\boldsymbol{p}}{\dd p_1}\right)\\&=\delta^3(\boldsymbol{p}-\boldsymbol{q})\frac{\gamma}{E_\boldsymbol{p}}\left(E_\boldsymbol{p}+v p_1\right)=\delta^3(\boldsymbol{p}-\boldsymbol{q})\frac{E_{\boldsymbol{p}’}}{E_\boldsymbol{p}}\end{aligned}$$

$$\ket{\boldsymbol{p}}=\sqrt{2E_\boldsymbol{p}}\;a_\boldsymbol{p}^\dagger\ket{0}$$

$$\braket{\boldsymbol{p}}{\boldsymbol{q}}=2E_\boldsymbol{p}(2\pi)^3\delta^3(\boldsymbol{p}-\boldsymbol{q})$$

如下测度在Lorentz变换下也不变

$$\int\frac{\text{d}^4p}{(2\pi)^3}\delta(p^2-m^2)\theta(p^0)=\int\frac{\text{d}^3p}{(2\pi)^3}\frac{1}{2E_\boldsymbol{p}}$$

可写出单粒子态恒等算符与位置本征态

$${\Large\mathbb{1}}\;=\int\frac{\text{d}^3p}{(2\pi)^3}\frac{1}{2E_\boldsymbol{p}}\ket{\boldsymbol{p}}\bra{\boldsymbol{p}}$$

$$\ket{\boldsymbol{x}}=\int\frac{\text{d}^3p}{(2\pi)^3}\frac{1}{2E_\boldsymbol{p}}e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}\ket{\boldsymbol{p}}\qquad \braket{\boldsymbol{x}}{\boldsymbol{p}}=e^{i\boldsymbol{p}\cdot\boldsymbol{x}}$$

位置本征态可由算符 $\phi$ 作用于真空态得到

$$\ket{\boldsymbol{x}}=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{p}}}(a_\boldsymbol{p}e^{i\boldsymbol{p}\cdot\boldsymbol{x}}+a_\boldsymbol{p}^\dagger e^{-i\boldsymbol{p}\cdot\boldsymbol{x}})\ket{0}=\phi(\boldsymbol{x})\ket{0}$$

Heisenberg绘景

Heisenberg绘景下态不变，算符随时间演化

$$\phi(x)=\phi(\boldsymbol{x},t)=e^{iHt}\phi(\boldsymbol{x})e^{-iHt}$$

利用Hamiltonian和产生湮灭算符的对易关系

$$e^{iHt}a_\boldsymbol{p}e^{-iHt}=a_\boldsymbol{p}e^{-iE_\boldsymbol{p}\,t}\qquad e^{iHt}a_\boldsymbol{p}^\dagger e^{-iHt}=a_\boldsymbol{p}^\dagger e^{iE_\boldsymbol{p}\,t}$$

$$\phi(x)=\phi(\boldsymbol{x},t)=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{p}}}(a_\boldsymbol{p}e^{-ip^\mu x_\mu}+a_\boldsymbol{p}^\dagger e^{ip^\mu x_\mu})$$

$$\pi(x)=\pi(\boldsymbol{x},t)=\frac{\partial\phi(\boldsymbol{x},t)}{\partial t}$$

若考虑动量算符和产生湮灭算符的对易关系

$$e^{i\boldsymbol{P}\cdot\boldsymbol{x}}a_\boldsymbol{p}e^{-i\boldsymbol{P}\cdot\boldsymbol{x}}=a_\boldsymbol{p}e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}\qquad e^{i\boldsymbol{P}\cdot\boldsymbol{x}}a_\boldsymbol{p}^\dagger e^{-i\boldsymbol{P}\cdot\boldsymbol{x}}=a_\boldsymbol{p}^\dagger e^{i\boldsymbol{p}\cdot\boldsymbol{x}}$$

$$\phi(x)=e^{iP^\mu x_\mu}\phi(0)e^{-iP^\mu x_\mu}$$

场算符遵循以下对易关系

$$[\phi(t,\boldsymbol{x}),\pi(t,\boldsymbol{y})]=i\delta^3(\boldsymbol{x}-\boldsymbol{y})$$

$$[\phi(t,\boldsymbol{x}),\phi(t,\boldsymbol{y})]=0=[\pi(t,\boldsymbol{x}),\pi(t,\boldsymbol{y})]$$

Feynman传播子

因果律

距离类空的两点发生的事件互不影响，因此两处的局域算符对易

$$[O(x),O(y)]=0$$

验证自由标量场理论满足因果律

$$\begin{aligned}\commutator{\phi(x)}{\phi(y)}&=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{p}}}\int\frac{\text{d}^3 q}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{q}}}[a_\boldsymbol{p}e^{-ip^\mu x_\mu}+a_\boldsymbol{p}^\dagger e^{ip^\mu x_\mu},a_\boldsymbol{q}e^{-iq^\mu y_\mu}+a_\boldsymbol{q}^\dagger e^{iq^\mu y_\mu}]\\&=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{2E_\boldsymbol{p}}(e^{-ip^\mu(x-y)_\mu}-e^{ip^\mu(x-y)_\mu})\\&=D(x-y)-D(y-x)\end{aligned}$$

$$D(x-y)=\bra{0}\phi(x)\phi(y)\ket{0}=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{2E_\boldsymbol{p}}e^{-ip^\mu(x-y)_\mu}$$

由于 $x,y$ 距离类空，Lorentz变换保持 $(x’-y’)^2=(x-y)^2<0 $，$x’-y’$ 在Lorentz变换下的轨迹形成单叶双曲面，因此可作Lorentz变换使得 $x-y\to y-x$，而 $D(x-y)$ Lorentz不变，即 $D(x-y)=D(y-x)$，因此 $\phi(x),\phi(y)$ 对易

然而两点的关联函数 $\bra{0}\phi(x)\phi(y)\ket{0}$ 非零，说明场在不同点的值存在关联，这是因为回溯足够长时间，这两点均处于某些事件的光锥之中，其历史并不互相独立，只是通过固定时空点的局部实验并不能获得这些联系

传播子

考虑时序两点函数，以下形式说明 $D_F(x-y)$ 将正频模式 $e^{-ip\cdot x}$沿时间向前传播，负频模式 $e^{ip\cdot x}$ 沿时间向后传播

$$\begin{aligned}D_F(x-y) &= \left\lbrace \begin{array}{l} D(x-y)&x^0>y^0\\D(y-x) &y^0>x^0 \end{array}\right.\equiv\bra{0}T\phi(x)\phi(y)\ket{0}\\&=\int\frac{\text{d}^3p}{(2\pi)^3}\frac{1}{2E_\boldsymbol{p}}e^{i\boldsymbol{p}\cdot(\boldsymbol{x}-\boldsymbol{y})}\left(\theta(x^0-y^0)e^{-iE_\boldsymbol{p}(x^0-y^0)}+\theta(y^0-x^0)e^{iE_\boldsymbol{p}(x^0-y^0)}\right)\end{aligned}$$

取如图所示围道，左右图围道分别记为$C_1,C_2$，可将传播子 $D_F(x-y)$ 中积分写为明显Lorentz不变的形式

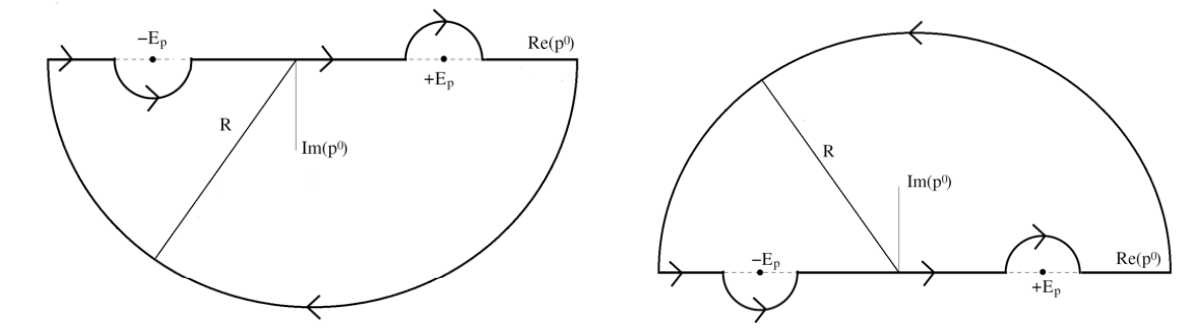
$$\begin{aligned}&\int_{-\infty}^\infty\frac{\dd p_0}{2\pi}\frac{i}{p^2-m^2}e^{-ip_0(x_0-y_0)}\\\quad\\=&\left\lbrace\begin{array}{l} \displaystyle\int_{C_1}\frac{\dd p_0}{2\pi}\frac{i}{(p^0)^2-E_\boldsymbol{p}^2}e^{-ip_0(x_0-y_0)}=\frac{1}{2E_\boldsymbol{p}}e^{-iE_\boldsymbol{p}(x^0-y^0)}&x^0>y^0\\ \displaystyle\int_{C_2}\frac{\dd p_0}{2\pi}\frac{i}{(p^0)^2-E_\boldsymbol{p}^2}e^{-ip_0(x_0-y_0)}=\frac{1}{2E_\boldsymbol{p}}e^{iE_\boldsymbol{p}(x^0-y^0)}&x^0<y^0\end{array}\right.\end{aligned}$$

$$D_F(x-y)=\int_C\frac{\text{d}^4p}{(2\pi)^4}\frac{i}{p^2-m^2}e^{-ip(x-y)}=\int\frac{\text{d}^4p}{(2\pi)^4}\frac{i}{p^2-m^2+i\epsilon}e^{-ip(x-y)}$$

其中为防止积分函数分母为零，在计算过程中将两个极点取为 $p^0=\pm(E_\boldsymbol{p}-i\epsilon)$，得到结果之后再令 $\epsilon\to 0$

$D_F(x-y)$ 为Klein-Gordon方程的格林函数

$$(\Box+m^2)D_F(x-y)=\int\frac{\text{d}^4p}{(2\pi)^4}\frac{i}{p^2-m^2+i\epsilon}(-p^2+m^2)e^{-ip(x-y)}=-i\delta^4(x-y)$$

可利用其得到微扰下运动方程的经典解

$$\mathcal{L}=\frac{1}{2}\partial_\mu\phi\partial^\mu\phi-\frac{1}{2}m\phi^2+J\cdot\phi$$

$$(\Box+m^2)\phi=J(x)$$

$$\phi_\text{cl}=i\int\text{d}^4yD_F(x-y)J(y)$$

若考虑将所有频率均沿时间向前传播或均向后传播，则得到提前或延迟格林函数

$$D_A(x-y)\equiv\theta(x^0-y^0)\bra{0}[\phi(x),\phi(y)]\ket{0}$$

$$D_R(x-y)\equiv\theta(y^0-x^0)\bra{0}[\phi(x),\phi(y)]\ket{0}$$

非相对论极限

非相对论极限下 $|\boldsymbol{p}|\ll m$，$E_\boldsymbol{p}=\sqrt{\boldsymbol{p}^2+m^2}\approx m$，Klein-Gordon方程近似解具有形式 $\phi_+(x)=e^{-imt}\varphi(x)$，代入方程得

$$i\frac{\partial \varphi}{\partial t}=-\frac{\nabla^2}{2m}\varphi$$

虽然形式与Schrodinger方程相同，但此时的$\varphi$为场算符而非波函数，二者含义有差别

此方程可由以下Lagrangian得到

$$\mathcal{L}=i\varphi^*\dot\varphi-\frac{1}{2m}\nabla\varphi^*\cdot\nabla\varphi\qquad\pi=\frac{\partial\mathcal{L}}{\partial\dot\varphi}=\varphi^*$$

$$\mathcal{H}=\frac{1}{2m}\nabla\varphi^*\cdot\nabla\varphi$$

波函数可由场算符对空间积分得到

$$\ket{\psi}=\int\text{d}^3x\;\psi(\boldsymbol{x})\ket{\boldsymbol{x}}=\int\text{d}^3x\;\psi(\boldsymbol{x})[\varphi(\boldsymbol{x})+\varphi^*(\boldsymbol{x})]\ket{0}$$

$$\varphi(\boldsymbol{x})=\int\frac{\text{d}^3p}{(2\pi)^3}a_\boldsymbol{p}e^{i\boldsymbol{p}\cdot\boldsymbol{x}}\qquad \varphi^*(\boldsymbol{x})=\int\frac{\text{d}^3p}{(2\pi)^3}a_\boldsymbol{p}^\dagger e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}$$

Hamiltonian作用于波函数可得，注意下式$a_\boldsymbol{p},a_\boldsymbol{p}^\dagger$对应于$\varphi(\boldsymbol{y})$，因此与$\psi(\boldsymbol{x})$对易

$$\begin{aligned}H\ket{\psi}&=\int\text{d}^3x\;\text{d}^3y\;\frac{1}{2m}\nabla\varphi^*(\boldsymbol{y})\cdot\nabla\varphi(\boldsymbol{y})\;\psi(\boldsymbol{x})\ket{\boldsymbol{x}}\\&=\int\frac{\text{d}^3x\;\text{d}^3q\;\text{d}^3p}{(2\pi)^6}\frac{\boldsymbol{p}^2}{2m}a_\boldsymbol{p}^\dagger a_\boldsymbol{p}\psi(\boldsymbol{x})a_\boldsymbol{q}^\dagger e^{-i\boldsymbol{q}\cdot\boldsymbol{x}}\ket{0}\\&=\int\frac{\text{d}^3x\;\text{d}^3p}{(2\pi)^3}\frac{\boldsymbol{p}^2}{2m}a_\boldsymbol{p}^\dagger e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}\psi(\boldsymbol{x})\ket{0}\\&=\int\text{d}^3x\left(-\frac{1}{2m}\nabla^2\psi\right)\ket{\boldsymbol{x}}\\&=-\frac{1}{2m}\nabla^2\ket{\psi}\end{aligned}$$

由此得Schrodinger方程

$$i\frac{\partial\ket{\psi}}{\partial t}=-\frac{1}{2m}\nabla^2\ket{\psi}$$