微扰展开
考虑如下 $\phi^4$ 场论,计算其两点关联函数,注意此时基态 $\ket{\Omega}\neq\ket{0}$
$$H=H_0+H_{\text{int}}=H_{\text{KG}}+\int\text{d}^3x\frac{\lambda}{4!}\phi^4$$
$$\bra{\Omega}T\phi(x)\phi(y)\ket{\Omega}$$
Heisenberg绘景下算符随时间演化
$$O_0(t,\boldsymbol{x})=e^{iH_0\,t}O(\boldsymbol{x})e^{iH_0\,t}\qquad O(t,\boldsymbol{x})=e^{iHt}O(\boldsymbol{x})e^{iHt}$$
$$O(t,\boldsymbol{x})=U^\dagger(t)O_0(t,\boldsymbol{x})U(t)\qquad U(t,t_0)=e^{iH_0(t-t_0)}e^{-iH(t-t_0)}$$
$$\frac{\dd U(t,t_0)}{\dd t}=-iH_I(t)U(t,t_0)\qquad H_I(t)=e^{iH_0(t-t_0)}H_\text{int}e^{-iH_0(t-t_0)}$$
由于$H_I$含时,无法将$U(t,t_0)$写为指数形式,故直接积分,从 $U^{(0)}(t,t_0)=1$ 开始迭代
$$U(t,t_0)=1+\frac{1}{i}\int_{t_0}^tH_I(t’)U(t’,t_0)\dd t’$$
$$U^{(1)}(t,t_0)=1+\frac{1}{i}\int_{t_0}^t\dd t_1H_I(t_1)U^{(0)}(t_1,t_0)$$
$$U^{(2)}(t,t_0)=1+\frac{1}{i}\int_{t_0}^t\dd t_2H_I(t_2)U^{(1)}(t_2,t_0)$$
$$U(t,t_0)=1+(-i)\int_{t_0}^t\dd t_1H_I(t_1)+(-i)^2\int_{t_0}^t\dd t_2H_I(t_2)\int_{t_0}^{t_2}\dd t_1H_I(t_1)+\cdots$$
采用时序排列$T$,可将$U(t,t_0)$写为指数形式
$$\begin{aligned}U(t,t_0)&=1+(-i)\int_{t_0}^t\dd t_1H_I(t_1)+(-i)^2\int_{t_0}^t\dd t_1\dd t_2T[H_I(t_1)H_I(t_2)]+\cdots\\&=T\left[\exp\left(-i\int_{t_0}^t\dd t’H_I(t’)\right)\right]\end{aligned}$$
现在可拓宽 $U$ 的定义,不再以 $t_0$ 为初始时刻
$$U(t,t’)=T\left[\exp\left(-i\int_{t’}^t\dd t’’H_I(t’’)\right)\right]$$
此式满足原来的微分方程,但初始条件变为 $U(t’,t’)=1$,可解得
$$i\frac{\partial U(t,t’)}{\partial t}=H_I(t)U(t,t’)$$
$$U(t,t’)=e^{iH_0(t-t_0)}e^{-iH(t-t’)}e^{-iH_0(t’-t_0)}$$
由以上形式可知当 $t_1\ge t_2\ge t_3$ 时
$$U(t_1,t_2)U(t_2,t_3)=U(t_1,t_3)\qquad U(t_1,t_3)U^\dagger(t_2,t_3)=U(t_1,t_2)$$
$\ket{\Omega}$和$\ket{0}$的关系
令$\ket{n}$为总Halmiltonian基态以外的本征态
$$H\ket{n}=E_n\ket{n}$$
$$e^{-iHT}\ket{0}=e^{-iE_\Omega T}\ket{\Omega}\bra{\Omega}\ket{0}+\sum_{\ket{n}}e^{-iE_n T}\ket{n}\bra{n}\ket{0}$$
由于$E_n>E_\Omega$,令$T\to\infty(1-i\epsilon)$,可将所有$\ket{n}$项舍弃
$$\begin{aligned}\ket{\Omega}&=\lim_{T\to\infty(1-i\epsilon)}(e^{-iE_\Omega T}\bra{\Omega}\ket{0})^{-1}e^{-iHT}\ket{0}\\&=\lim_{T\to\infty(1-i\epsilon)}(e^{-iE_\Omega (t_0-(-T))}\bra{\Omega}\ket{0})^{-1}e^{-iH(t_0-(-T))}e^{-iH_0(-T-t_0)}\ket{0}\\&=\lim_{T\to\infty(1-i\epsilon)}(e^{-iE_\Omega (T+t_0)}\bra{\Omega}\ket{0})^{-1}U(t_0,-T)\ket{0}\end{aligned}$$
对左矢同样有
$$\bra{\Omega}=\lim_{T\to\infty(1-i\epsilon)}\bra{0}U(T,t_0)(e^{-iE_\Omega (T-t_0)}\bra{0}\ket{\Omega})^{-1}$$
现在可计算关联函数,假设 $x^0\ge y^0\ge t_0$
$$\begin{aligned}\bra{\Omega}\phi(x)\phi(y)\ket{\Omega}=&\lim_{T\to\infty(1-i\epsilon)}(e^{-2iE_\Omega T}|\bra{0}\ket{\Omega}|^2)^{-1}\times\\&\bra{0}U(T,x^0)\phi_0(x)U(x^0,y^0)\phi_0(y)U(y^0,-T)\ket{0}\end{aligned}$$
$$\bra{\Omega}\ket{\Omega}=\lim_{T\to\infty(1-i\epsilon)}(e^{-2iE_\Omega T}|\bra{0}\ket{\Omega}|^2)^{-1}\bra{0}U(T,-T)\ket{0}=1$$
$$\bra{\Omega}\phi(x)\phi(y)\ket{\Omega}=\lim_{T\to\infty(1-i\epsilon)}\frac{\bra{0}U(T,x^0)\phi_0(x)U(x^0,y^0)\phi_0(y)U(y^0,-T)\ket{0}}{\bra{0}U(T,-T)\ket{0}}$$
$$\bra{\Omega}T\phi(x)\phi(y)\ket{\Omega}=\lim_{T\to\infty(1-i\epsilon)}\frac{\displaystyle\bra{0}T\left[\phi_0(x)\phi_0(y)\exp\left(-i\int_{-T}^{T}\dd t H_I(t)\right)\right]\ket{0}}{\displaystyle\bra{0}T\left[\exp\left(-i\int_{-T}^{T}\dd t H_I(t)\right)\right]\ket{0}}$$
Wick定理
为计算以下时序多点关联函数,将场分为两部分,下文在$\bra{0}$和$\ket{0}$中的$\phi$均为自由场$\phi_0$
$$\bra{0}T\phi(x_1)\phi(x_2)\cdots\phi(x_n)\ket{0}$$
$$\phi(x)=\phi^+(x)+\phi^-(x)$$
$$\phi^+(x)=\int\frac{\text{d}p^3}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{p}}}a_\boldsymbol{p}e^{-ip\cdot x}\qquad \phi^-(x)=\int\frac{\text{d}p^3}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{p}}}a_\boldsymbol{p}^\dagger e^{ip\cdot x}$$
$$\phi^+(x)\ket{0}=0=\bra{0}\phi^-(x)$$
直接计算知两个场的时序乘积与正规序乘积的关系为
$$T\phi(x)\phi(y)=N\phi(x)\phi(y) + \overbracket{\phi(x)\phi}(y) $$
$$\overbracket{\phi(x)\phi}(y)=\left\lbrace\begin{array}{l} [\phi^+(x),\phi^-(y)]&x^0>y^0\\ [\phi^+(y),\phi^-(x)]&y^0>x^0\end{array}\right.=D_F(x-y)$$
由归纳法可得 Wick定理
$$T[\phi(x_1)\phi(x_2)\cdots\phi(x_n)]=N[\phi(x_1)\phi(x_2)\cdots\phi(x_n)+所有可能的缩并]$$
正规序排列下,含未缩并的$\phi$的项与真空态作内积后为零,对于四点关联函数$\bra{0}T\phi(x_1)\phi(x_2)\phi(x_3)\phi(x_4)\ket{0}$,其值如下
$$D(x_1-x_2)D(x_3-x_4)+D(x_1-x_3)D(x_2-x_4)+D(x_1-x_4)D(x_2-x_3)$$
Feymann图
将两点关联函数分子展开,其零阶项即为$D_F(x-y)$,对于$\phi^4$理论,$H_I=\displaystyle\frac{\lambda}{4!}\phi^4$,其一阶项如下
$$\begin{aligned}&\quad\bra{0}T\left[\phi(x)\phi(y)\left(-i\int\dd t H_I(t)\right)\right]\ket{0}\\&=\bra{0}T\left[\phi(x)\phi(y)\left(-\frac{i\lambda}{4!}\right)\int\text{d}^4z\;\phi(z)\phi(z)\phi(z)\phi(z)\right]\ket{0}\\&=3\left(-\frac{i\lambda}{4!}\right)D_F(x-y)\int\text{d}^4z\;D_F(z-z)D_F(z-z)\\&+12\left(-\frac{i\lambda}{4!}\right)\int\text{d}^4z\;D_F(x-z)D_F(y-z)D_F(z-z)\end{aligned}$$
对$D_F(x-y)$,用连接$x,y$两点的线表示;对$D_F(z-z)$,用经过$z$点的圈表示,可得上式的Feymann图
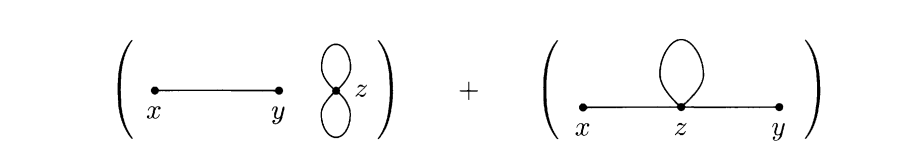
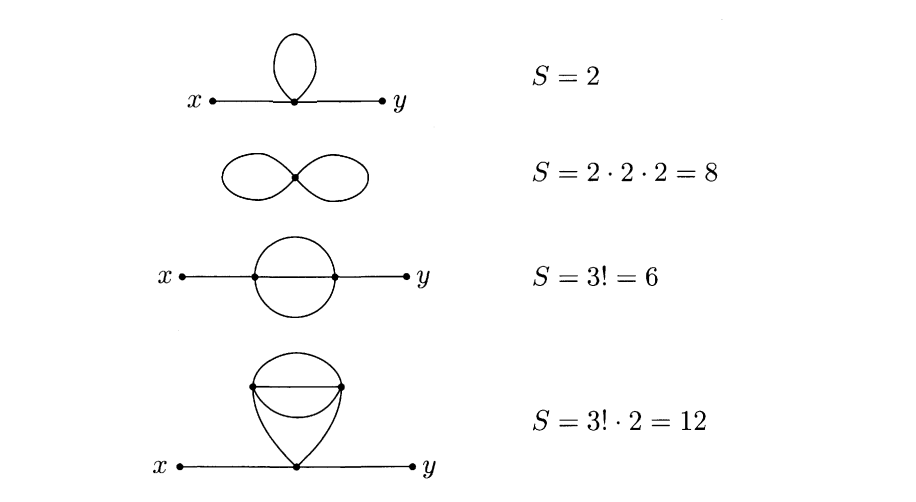
对于单个Feymann图,交换其中某些线或者圈使图不变的方法数乘上每个圈自带的端点重数$2$称为此图的对称因子
由于相同的缩并方法数相当于将含$n$个$\phi(z)$的项分成两个一组的方法数,对称因子相当于交换仅含$\phi(z)$的组与交换组内$\phi(z)$的方法数,二者相乘即为$n$个$\phi(z)$的全排列$n!$,由于$H_I$的$n$阶相互作用项$\phi^n$自带$1/n!$的系数,因此Feymann图对应的积分的系数即为$1$除以此图的对称因子
以下为一些Feymann图的对称因子
若不只考虑关联函数分子的一阶项,
散射截面与S矩阵
定义散射截面$\sigma$
$$\sigma=\frac{散射到某立体角内的粒子数}{入射粒子束数密度\times速度\times时间}$$
考虑粒子的散射过程,记$\ket{i}_\text{in},\ket{f}_\text{out}$分别为散射前后粒子的动量本征态,out和in表示时间趋于正负无穷,定义S矩阵
$$_{\text{out}}\braket{f}{i}_\text{in}=\lim_{T\to\infty}\bra{f}e^{-2iHT}\ket{i}=\bra{f}S\ket{i}$$
$$\bra{f}S\ket{i}=S_{fi}$$
由此定义知$S$为酉阵,由下式知其与概率守恒等价
$$\sum_f|\bra{f}S\ket{i}|^2=\sum_f\bra{i}S^\dagger\ket{f}\bra{f}S\ket{i}=\bra{i}S^\dagger S\ket{i}=1$$
若散射中粒子无相互作用,则$S$为单位阵,故将其写为单位阵与相互作用成分之和
$$S=1+iT$$
散射过程满足四维动量守恒,因此$T$具有以下形式,其中矩阵元$\mathcal{M}_{fi}$相当于散射振幅
$$T_{fi}=(2\pi)^4\delta^4(\sum p_f-\sum p_i)\mathcal{M}_{fi}$$
将波函数用动量本征态展开,可知从$\ket{\psi_i}$态散射到动量空间中 $\displaystyle\prod_f\text{d}^3 p_f$ 区域的概率
$$\ket{\psi}=\int\frac{\text{d}^3k}{(2\pi)^3}\frac{1}{\sqrt{2E_\boldsymbol{k}}}\psi(\boldsymbol{k})\ket{\boldsymbol{k}}$$
$$\braket{\psi}{\psi}=1\qquad\int\frac{\text{d}^3k}{(2\pi)^3}|\psi(\boldsymbol{k})|^2=1$$
$$\mathcal{P}=\prod_f\frac{\text{d}^3 p_f}{(2\pi)^3 2E_{p_f}}|_{\text{out}}\bra{f}\ket{\psi_i}_{\text{in}}|^2$$
2 $\boldsymbol{\to}$ n $\quad$考虑单个$A$粒子对$B$粒子束的散射,记$l$为碰撞参数,则散射截面为
$$\dd\sigma=\int\text{d}^2l\;\mathcal{P}(l)$$
$$=\left(\prod_f\frac{\text{d}^3 p_f}{(2\pi)^3 2E_{p_f}}\right)\int\text{d}^2l\left(\prod_{i=A,B}\int\frac{\text{d}^3p_i}{(2\pi)^3}\frac{\psi_i(\boldsymbol{p_i})}{\sqrt{2E_\boldsymbol{p_i}}}\int\frac{\text{d}^3p_i’}{(2\pi)^3}\frac{\psi_i(\boldsymbol{p_i’})}{\sqrt{2E_\boldsymbol{p_i’}}}\right)e^{i\boldsymbol{l}\cdot(\boldsymbol{p_B}-\boldsymbol{p’_B})}S_{fi}S_{i’f}$$
舍弃散射截面中向前散射的无相互作用部分,将其用$\mathcal{M}_{fi}$表示出来,取质心参考系
$$\dd\sigma=\frac{|\mathcal{M}_{fi}|^2}{4E_AE_B|\boldsymbol{v}_A-\boldsymbol{v}_B|}\dd\Pi\qquad E_AE_B|\boldsymbol{v}_A-\boldsymbol{v}_B|=|\boldsymbol{p}_i|E_\text{cm}$$
$$\dd\Pi=\prod_f\frac{\text{d}^3 p_f}{(2\pi)^3 2E_{p_f}}(2\pi)^4\delta^4(\sum p_f-\sum p_i)$$
2 $\boldsymbol{\to}$ 2 $\quad$对测度$\dd\Pi$积分,同样取质心参考系,得微分散射截面
$$\int\dd\Pi=\int\dd\Omega\frac{|\boldsymbol{p}_f|}{16\pi^2 E_\text{cm}}$$
$$\left(\frac{\dd\sigma}{\dd\Omega}\right)_\text{CM}=\frac{|\mathcal{M}_{fi}|^2}{64\pi^2E_\text{cm}^2}\frac{|\boldsymbol{p}_f|}{|\boldsymbol{p}_i|}$$
若散射中四个粒子质量相等,则简化为
$$\left(\frac{\dd\sigma}{\dd\Omega}\right)_\text{CM}=\frac{|\mathcal{M}_{fi}|^2}{64\pi^2E_\text{cm}^2}$$
1 $\boldsymbol{\to}$ n $\quad$对于单粒子衰变,由 2 $\to$ n 散射截面表达式可知衰变率为
$$\dd\Gamma=\frac{|\mathcal{M}(m_i\to f)|^2}{2m_i}\dd\Pi$$
光学定理$\quad$由 $S^\dagger S=1$
$$i(T-T^\dagger)=T^\dagger T$$
$$\bra{f}T^\dagger T\ket{i}=\sum_n\left(\prod_{m=1}^n\int\frac{\text{d}^3 p_m}{(2\pi)^3 2E_{p_m}}\right)\bra{f}T^\dagger\ket{n}\bra{n} T\ket{i}$$
$$\mathcal{M}_{fi}-\mathcal{M}_{if}^*=i\sum_n \int\dd\Pi_n \mathcal{M}_{fn}^*\mathcal{M}_{in}$$
$$\dd\Pi_n=\prod_n\frac{\text{d}^3 p_n}{(2\pi)^3 2E_{p_n}}(2\pi)^4\delta^4(\sum p_f-\sum p_i)$$
2 $\boldsymbol{\to}$ anything$\quad$若取$\ket{f}=\ket{i}$,由等式形式可知两个粒子碰撞的总散射截面
$$2\Im\;\mathcal{M}_{ii}=\sum_n \int\dd\Pi_n|\mathcal{M}_{in}|^2$$
$$\sigma_\text{tot}(i\to\text{anything})=\frac{\mathcal{M}_{ii}}{2E_\text{cm}|\boldsymbol{p}_i|}$$
LSZ约化公式
Lehmann-Symanzik-Zimmermann约化公式 建立了关联函数和散射矩阵的联系
将$\ket{i}_\text{in}$,$\ket{f}_\text{out}$写为产生湮灭算符的形式,注意下文中的$\phi$并非自由场
$$\ket{i}_\text{in}=\prod_i\sqrt{2E_{p_i}}a_{p_i}^\dagger(-\infty)\ket{\Omega}\qquad\ket{f}_\text{out}=\prod_f\sqrt{2E_{p_f}}a_{p_f}^\dagger(\infty)\ket{\Omega}$$
$$S_{fi}=\left(\prod_{f}\sqrt{2E_{f}}\prod_{i}\sqrt{2E_{i}}\right)\bra{\Omega}\prod_f a_{p_f}(\infty)\prod_i a_{p_i}^\dagger(-\infty)\ket{\Omega}$$
同样将$\phi$写为产生湮灭算符的形式
$$\phi(x)=\int\frac{\text{d}^3 p}{(2\pi)^3}\frac{1}{\sqrt{2E_p}}[a_p(t) e^{-ipx}+a_p^\dagger(t) e^{ipx}]$$
$$\begin{aligned}&\quad i\int\text{d}^4 x\;e^{ipx}(\Box+m^2)\phi(x)=i\int\text{d}^4 x\;e^{ipx}(\partial_t^2+E_p^2)\phi(x)\\&=\int\text{d}^4 x\;\partial_t[e^{ipx}(i\partial_t+E_p)\phi(x)]=\int\dd t\;\partial_t\left[e^{iE_pt}\int\text{d}^3x\;e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}(i\partial_t+E_p)\phi(x)\right]\end{aligned}$$
由于积分为全导数形式,仅与 $t=\pm\infty$ 的值有关,此时 $a,a^\dagger$ 为自由场产生湮灭算符,故可在式中令 $\partial_t a(t)=0$,继续积分
$$\begin{aligned}&\quad\int\text{d}^3x\;e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}(i\partial_t+E_p)\phi(x)\\&=\int\text{d}^3x\;e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}(i\partial_t+E_p)\int\frac{\text{d}^3 k}{(2\pi)^3}\frac{1}{\sqrt{2E_k}}[a_k(t) e^{-ikx}+a_k^\dagger(t) e^{ikx}]\\&=\int\frac{\text{d}^3 k}{(2\pi)^3}\int\text{d}^3x\left[\left(\frac{E_k+E_p}{\sqrt{2E_k}}\right)a_k(t)e^{-ikx}e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}+\left(\frac{-E_k+E_p}{\sqrt{2E_k}}\right)a_k^\dagger(t)e^{ikx}e^{-i\boldsymbol{p}\cdot\boldsymbol{x}}\right]\\&=\sqrt{2E_p}a_p(t)e^{-iE_pt}\color{white}{\int}\end{aligned}$$
代入原积分,利用此结果即得LSZ约化公式
$$i\int\text{d}^4 x\;e^{ipx}(\Box+m^2)\phi(x)=\sqrt{2E_p}[a_p(\infty)-a_p(-\infty)]$$
$$\begin{aligned} S_{fi}&=\left(\prod_{f}\sqrt{2E_{f}}\prod_{i}\sqrt{2E_{i}}\right)\bra{\Omega}T\left\{\prod_f a_{p_f}(\infty)\prod_i a_{p_i}^\dagger(-\infty)\right\}\ket{\Omega}\\&=\left(\prod_{f}\sqrt{2E_{f}}\prod_{i}\sqrt{2E_{i}}\right)\bra{\Omega}T\left\{\prod_f [a_{p_f}(\infty)-a_{p_f}(-\infty)]\prod_i [a_{p_i}^\dagger(\infty)-a_{p_i}^\dagger(-\infty)]\right\}\ket{\Omega}\\&=\prod_f\left[i\int\text{d}^4 x_f\;e^{ip_fx_f}(\Box_f+m^2)\right]\prod_i\left[i\int\text{d}^4 x_i\;e^{-ip_ix_i}(\Box_i+m^2)\right]\bra{\Omega}T\left\{\prod_f\phi(x_f)\prod_i\phi(x_i)\right\}\ket{\omega}\end{aligned}$$