QED重整化

高能QED裸Lagrangian

$$\mathcal{L}=-\frac{1}{4}(F_{\mu\nu})^2+\bar\psi(i\cancel{\partial}-m_0)\psi-e_0\bar\psi\gamma^\mu\psi A_\mu$$

单电子和单光子传播子费曼图

定义重整化场，消去Feymann规则中的 $Z_2,Z_3$

$$\psi=Z_2^{1/2}\psi_r\qquad A^\mu=Z_3^{1/2}A^\mu_r$$

$$\mathcal{L}=-\frac{Z_3}{4}(F_{\mu\nu})_r^2+Z_2\bar\psi_r(i\cancel{\partial}-m_0)\psi_r-Z_2 Z_3^{1/2}e_0\bar\psi_r\gamma^\mu\psi_r A_{\mu}^r$$

利用低能下的观测电荷 $e$ 与质量 $m$，省略重整化角标 $r$，可将Lagrangian写为低能物理项与微扰项之和

$$Z_2Z_3^{1/2}e_0=e’=Z_1 e\qquad Z_2 m_0=m+\delta_m$$

$$Z_i=1+\delta_i$$

$$\mathcal{L}=\left(-\frac{1}{4}F_{\mu\nu}^2+\bar\psi(i\cancel{\partial}-m)\psi-e\bar\psi\gamma^\mu\psi A_\mu\right)+\left(-\frac{\delta_3}{4}F_{\mu\nu}^2+\bar\psi(i\delta_2\cancel{\partial}-\delta_m)\psi-e\delta_1\bar\psi\gamma^\mu\psi A_\mu\right)$$

下文计算单圈修正下的 $Z_i$，可得出电荷与质量对能标的依赖关系

反常磁矩

计算以下Feymann图，图中均为重整化场，虚光子 $q^2<0$ ，令 $\Gamma^\mu=\gamma^\mu+\delta_\alpha \Gamma^\mu$，在 $\alpha$ 一阶修正下

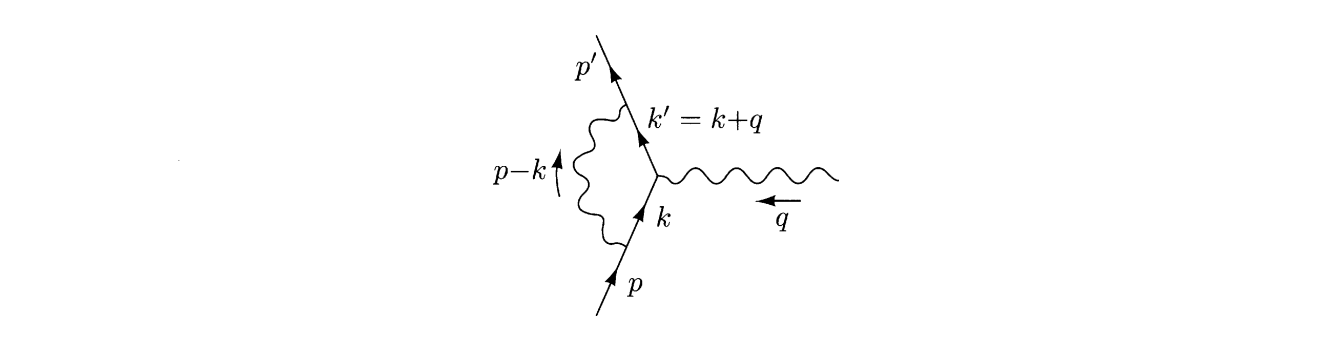
$$\begin{aligned}&=\bar u(p’)\delta_\alpha\Gamma^\mu(p’,p) u(p)\\\quad\\&=\int\frac{\text{d}^4 k}{(2\pi)^4}\frac{-ig_{\nu\rho}}{(k-p)^2}\bar u(p’)(-ie\gamma^\nu)\frac{i(\cancel{k’}+m)}{k’^2-m^2}\gamma^\mu\frac{i(\cancel{k}+m)}{k^2-m^2}(-ie\gamma^\rho)u(p)\\\quad\\&=2i e^2\int\frac{\text{d}^4 k}{(2\pi)^4}\frac{\bar u(p’)[\cancel{k}\gamma^\mu\cancel{k’}+m^2\gamma^\mu-2m(k+k’)^\mu]u(p)}{(k-p)^2(k’^2-m^2)(k^2-m^2)}\end{aligned}$$

计算中用到了以下等式

$$\{\cancel{a},\cancel{b}\}=2ab\qquad \gamma^\nu\gamma^\mu\gamma_\nu=-2\gamma^\mu\qquad \{\gamma^\mu,\cancel{a}\}=2a^\mu$$

在计算积分之前，可将 $\Gamma^\mu$ 进一步简化，将 $\Gamma^\mu$ 写为以下形式

$$\Gamma^\mu=A\gamma^\mu+B(p’+p)^\mu+C(p’-p)^\mu$$

由Dirac方程，低能下可用 $m$ 替代 $\cancel{p’},\cancel{p}$，因此 $\Gamma^\mu$ 系数仅与 $q^2$ 有关；由Ward等式，$\mathcal{M}^\mu q_\mu=0$，因此 $C=0$；再由Gordon等式，可将 $\Gamma^\mu$ 写为以下形式

$$\bar u(p’)\gamma^\mu u(p)=\bar u(p’)\left[\frac{p’^\mu+p^\mu}{2m}+\frac{i\sigma^{\mu\nu}q_\nu}{2m}\right]u(p)\qquad\sigma^{\mu\nu}=\frac{i}{2}[\gamma^\mu,\gamma^\nu]$$

$$\Gamma^\mu=\gamma^\mu F_1(q^2)+i\frac{\sigma^{\mu\nu}q_\nu}{2m}F_2(q^2)$$

由 $e’=Z_1 e$ 可得重整化条件

$$-iZ_1e\;\Gamma^\mu(q=0)=-ie\gamma^\mu\qquad\Gamma^\mu(q=0)=Z_1^{-1}\gamma^\mu$$

用 $F_1,F_2$ 表示重整化 Dirac Lagrangian

$$\begin{aligned}\mathcal{L}_{\text{Dirac}}&=\bar\psi(i\gamma^\mu(\partial_\mu+ieA_\mu)-m)\psi\\&=\bar\psi(i\cancel{\partial}-m)\psi-e\bar\psi\gamma^\mu F_1(0)A_\mu\psi -e\bar\psi\left(\frac{\sigma^{\mu\nu}}{2m}F_2(0)\partial_\nu A_\mu\right)\psi\end{aligned}$$

Dirac方程平方成为

$$\left[(i\partial_\mu-eF_1(0)A_\mu)^2-m^2+\frac{e}{2}\sigma^{\mu\nu}F_{\mu\nu}(1+F_2(0))+\cdots\right]\psi=0$$

Feymann参数

$$\frac{1}{A_1 A_2\cdots A_n}=\int_0^1\dd x_1\dd x_2\cdots\dd x_n\;\delta(\sum_{i=1}^n x_i-1)\frac{(n-1)!}{[x_1A_1+x_2A_2+\cdots+x_n A_n]^n}$$

$$\frac{1}{(k-p)^2(k’^2-m^2)(k^2-m^2)}=\int_0^1\dd x\dd y\dd z\;\delta(x+y+z-1)\frac{2}{D^3}$$

$$D=l^2-\Delta$$

$$l=k+yq-zp\qquad \Delta=-xy q^2+(1-z)^2m^2$$