正规序

初级场OPE仅含一项奇异项，因此两个初级场算符乘积的正规化只需简单减去其真空期望，亦即Wick定理；而对于非初级场算符，此方法不再适用

写出算符 $A(z)B(w)$ OPE，并将 $A(z)B(z)$ 正规序记为 $(AB)(z)$

$$A(z)B(w)=\sum_{n=\infty}^N\frac{\{AB\}_n(w)}{(z-w)^n}$$

$$(AB)(w)=\{AB\}_0(w)$$

定义 $A(z)B(w)$ 的缩并为其OPE中所有奇异项；$(A(z)B(w))$ 为所有正规项，因此可用正规序Taylor展开

$$\overbracket{A(z)B}(w)\equiv\sum_{n=1}^N\frac{\{AB\}_n(w)}{(z-w)^n}$$

$$(A(z)B(w))=\sum_{k\ge 0}\frac{(z-w)^k}{k!}(\partial^k AB)(w)$$

$$A(z)B(w)=\overbracket{A(z)B}(w)+(A(z)B(w))$$

正规序现在可写为

$$(AB)(w)=\lim_{z\to w}\left[A(z)B(w)-\overbracket{A(z)B}(w)\right]$$

$$(AB)(w)=\frac{1}{2\pi i}\oint_w\frac{\dd z}{z-w}A(z)B(w)$$

将 $\phi(z)$，$T(z)$ 在 $w$ 附近Laurent展开

$$\phi(z)=\sum_{n\in \mathbb{Z}}(z-w)^{-n-h}\phi_n(w)$$

$$T(z)=\sum_{n\in \mathbb{Z}}(z-w)^{-n-2}L_n(w)$$

由此形式可得 $T(z)$ 与任意场 $A(w)$ 的OPE

$$T(z)A(w)=\sum_{n\in\mathbb{Z}}(z-w)^{-n-2}(L_n A)(w)$$

写出其中几项具体形式

$$T(z)A(w)=\cdots+\frac{h_A A(w)}{(z-w)^2}+\frac{\partial A(w)}{z-w}+(TA)(w)+(z-w)(\partial T A)(w)+\cdots$$

比较可知

$$(L_0A)(w)=h_A A(w)$$

$$(L_{-1} A)(w)=\partial A(w)$$

$$(L_{-n-2}A)(w)=\frac{1}{n!}(\partial^n T A)(w)$$

$$(L_{-n-2}\mathbb{I})(w)=\frac{1}{n!}\partial^n T (w)$$

注意到正规序积分表达式中为径序

$$\frac{1}{2\pi i}\oint_w\frac{\dd z}{z-w}A(z)B(w)=\frac{1}{2\pi i}\oint_{|z|>|w|}\frac{\dd z}{z-w}A(z)B(w)-\frac{1}{2\pi i}\oint_{|z|<|w|}\frac{\dd z}{z-w}B(w)A(z)$$

先考虑第一项，将 $A(z)$，$B(w)$ 在 $x$ 附近Laurent展开，$|z|>|x|>|w|$

$$A(z)=\sum_n(z-x)^{-n-h_A}A_n(x)$$

$$B(w)=\sum_n(w-x)^{-p-h_B}B_p(x)$$

由 $z-w=(z-x)-(w-x)$ 有

$$\frac{1}{z-w}=\sum_{l\ge 0}\frac{(w-x)^l}{(z-x)^{l+1}}$$

第一项成为

$$\begin{aligned}&\frac{1}{2\pi i}\oint_{|z|>|w|}\frac{\dd z}{z-w}A(z)B(w)\\=&\frac{1}{2\pi i}\oint\dd z\sum_{n,p;l\ge 0}(w-x)^{l-p-h_B}(z-x)^{-n-h_A-l-1}A_n(x)B_p(x)\\=&\sum_{p;n\le -h_A}(w-x)^{-n-p-h_A-h_B}A_n(x)B_p(x)\end{aligned}$$

同理第二项为

$$\begin{aligned}&\frac{1}{2\pi i}\oint_{|z|<|w|}\frac{\dd z}{z-w}A(z)B(w)\\=&\frac{1}{2\pi i}\oint\dd z\sum_{n,p;l\ge 0}(w-x)^{-l-1-p-h_B}(z-x)^{l-n-h_A}B_p(x)A_n(x)\\=&\sum_{p;n> -h_A}(w-x)^{-n-p-h_A-h_B}B_p(x)A_n(x)\end{aligned}$$

结合两项可得

$$(AB)_m=\sum_{n\le -h_A}A_n B_{m-n}+\sum_{n>-h_A}B_{m-n}A_n$$

$$(AB)(z)=\sum z^{-n-h_A-h_B}(AB)_n$$

上式中正规序与 $:\;:$ 不同，其不满足交换律与结合律

$$(AB)(z)\neq (BA)(z)$$

$$((AB)C)(z)\neq (A(BC))(z)$$

裔场

考虑 $\ket{h}$ 的裔 $L_{-n}\ket{h}$ 的积分表示

$$L_{-n}\ket{h}=L_{-n}\phi(0)\ket{0}=\frac{1}{2\pi i}\oint\frac{\dd z}{z^{n-1}}T(z)\phi(0)\ket{0}$$

由 $\displaystyle T(z)A(w)=\sum_{n\in\mathbb{Z}}(z-w)^{-n-2}(L_n A)(w)$ 知上式即为 $(L_{-n}\phi)(0)\ket{0}$

由此可定义对应 $L_{-n}\ket{h}$ 的裔场 $\phi^{(-n)}(w)$

$$\phi^{(-n)}(w)\equiv(L_{-n}\phi)(w)=\frac{1}{2\pi i}\oint_w\frac{\dd z}{(z-w)^{n-1}}T(z)\phi(w)$$

$$\phi^{(0)}(w)=h\phi(w)\qquad \phi^{(-1)}(w)=\partial\phi(w)$$

裔场的关联函数可由其祖初级场得出，考虑 $\ev{(L_{-n}\phi(w)X)}=\ev{\phi^{(-n)}(w)X}$ ，其中 $X=\phi_1(w_1)\cdots\phi_N(w_N)$

$$\begin{aligned}\ev{\phi^{(-n)}(w)X}&=\frac{1}{2\pi i}\oint_w\frac{\dd z}{(z-w)^{n-1}}\ev{T(z)\phi(w)X}\\&=-\frac{1}{2\pi i}\oint_{\{w_i\}}\frac{\dd z}{(z-w)^{n-1}}\sum_i\left[\frac{1}{z-w_i}\partial_{w_i}\ev{\phi(w)X}+\frac{h_i}{(z-w_i)^2}\ev{\phi(w)X}\right]\\&=\mathcal{L}_{-n}\ev{\phi(w)X}\end{aligned}$$

$$\mathcal{L}_{-n}=\sum_i\left[\frac{(n-1)h_i}{(w_i-w)^n}-\frac{1}{(w_i-w)^{n-1}}\partial_{w_i}\right]$$

由平移不变性，$\displaystyle\partial_w+\sum_i\partial_{w_i}$ 对关联函数作用为零，可知 $\mathcal{L}_{-1}=\partial_w$

由单指标裔场可定义多指标裔场

$$\phi^{(-k,-n)}(w)=(L_{-k}L_{-n})(w)=\frac{1}{2\pi i}\oint_w\frac{\dd z}{(z-w)^{k-1}}T(z)(L_{-n}\phi)(w)$$

$$\phi^{(0,-n)}(w)=(h+n)\phi^{(-n)}(w)\qquad\phi^{(-1,-n)}(w)=\partial_w\phi^{(-n)}(w)$$

多指标裔场关联函数同样可以通过 $\mathcal{L}_{-n}$ 作用于祖初级场关联函数得到

$$\ev{\phi^{-k_1,\cdots,-k_n}(w)X}=\mathcal{L}_{-k_1}\cdots\mathcal{L}_{-k_n}\ev{\phi(w)X}$$

共形族

初级场 $\phi$ 与其所有裔场构成的集合称为共形族，记作 $[\phi]$，共形族在共形变换下保持封闭性，因此 $T(z)$ 与共形族中场的OPE可分解为共形族中其他场

将OPE写为以下两部分

$$T(z)\phi^{(-n)}(w)=\sum_{k\ge 0}(z-w)^{k-2}(L_{-k}\phi^{(-n)})(w)+\sum_{k>0}\frac{1}{(z-w)^{k+2}}(L_k\phi^{(-n)})(w)$$

其中第一部分由裔场 $\phi^{(-k,-n)}$ 构成；第二部分由三阶以上极点奇异项构成，可通过以下 $TT$ OPE计算

$$\begin{aligned}T(z)\phi^{(-n)}(w)&=\frac{1}{2\pi i}\oint_w\frac{\dd x}{(x-w)^{n-1}}T(z)T(x)\phi(w)\\&\sim\frac{1}{2\pi i}\oint_w\frac{\dd x}{(x-w)^{n-1}}\left[\frac{c/2}{(z-x)^4}+\frac{2 T(x)}{(z-x)^2}+\frac{\partial T(x)}{z-x}\right]\phi(w)\\&=\frac{cn(n^2-1)/12}{(z-w)^{n+2}}\phi(w)+\oint_w\frac{\dd x}{(x-w)^{n-1}}\sum_{l=0}^\infty\phi^{(-l)}(w)\left[\frac{2(x-w)^{l-2}}{(z-x)^2}+\frac{(l-2)(x-w)^{l-3}}{z-x}\right]\\&=\frac{cn(n^2-1)/12}{(z-w)^{n+2}}\phi(w)+\sum_{l=0}^{n+1}\frac{2n-l}{(z-w)^{n+2-l}}\phi^{(-l)}(w)\end{aligned}$$

组合两部分，得到 $T\phi^{-n}$ OPE

$$T(z)\phi^{(-n)}(w)=\frac{cn(n^2-1)/12}{(z-w)^{n+2}}\phi(w)+\sum_{k=1}^{n}\frac{n+k}{(z-w)^{k+2}}\phi^{(k-n)}(w)+\sum_{k\ge 0}(z-w)^{k-2}\phi^{(-k,-n)}(w)$$

对于 $T(z)\phi^{(-1)}(w)=T(z)\partial\phi(w)$

$$T(z)\partial\phi(w)\sim \frac{2h\phi(w)}{(z-w)^3}+\frac{(h+1)\partial\phi(w)}{(z-w)^2}+\frac{\partial^2\phi(w)}{z-w}$$

初级场的裔称为次级场，其在共形变换 $z\to f(z)$ 下变换规律为

$$A(z)\to\left(\frac{\dd f}{\dd z}\right)^{h’}A(f(z))+\text{extra terms}\qquad h’=h+n\;\;(n>0)$$

算符代数

由共性不变性可以定出初级场关联函数形式，其中 $\phi_\alpha,\phi_\beta$ 共形维数相同

$$\ev{\phi_\alpha(w,\bar w)\phi_\beta(z,\bar z)}=\frac{C_{\alpha\beta}}{(w-z)^{2h}(\bar w-\bar z)^{2\bar h}}$$

$C_{\alpha\beta}$ 为对称阵，因此可选取一组基使得 $C_{\alpha\beta}=\delta_{\alpha\beta}$，下文默认使用此归一化

通过合适的全局共形变换将关联点变为 $w=\infty,z=0$，场成为渐近态，两点关联函数成为Hilbert空间中的双线性乘积，其中最高权态的正交性隐含了两个场裔即Verma模的正交性

$$\lim_{w,\bar w\to\infty}w^{2h}\bar w^{2\bar h}\ev{\phi(w,\bar w)\phi’(0,0)}=\braket{h}{h’}\braket{\bar h}{\bar h’}$$

共形维数不变要求算符代数具有以下形式，其中 $K=\sum_i k_i，\bar K=\sum_i \bar k_i$

$$\phi_1(z,\bar z)\phi_2(0,0)=\sum_p\sum_{\{k,\bar k\}}C_{12}^{p\{k,\bar k\}}z^{h_p-h_1-h_2+K}\bar z^{\bar h_p-\bar h_1-\bar h_2+\bar K}\phi_p^{\{k,\bar k\}}(0,0)$$

在两点关联函数中插入第三个初级场，由三点关联函数形式可知

$$\begin{aligned}\bra{\phi_r}\phi_1(z,\bar z)\ket{\phi_2}&=\lim_{w,\bar w\to\infty}w^{2h}\bar w^{2\bar h}\ev{\phi_r(w,\bar w)\phi_1(z,\bar z)\phi_2(0,0)}\\&=\frac{C_{r12}}{z^{h_1+h_2-h_r}\bar z^{\bar h_1+\bar h_2-\bar h_r}}\end{aligned}$$

与上文算符OPE比较，由Vermam模的正交性知唯一的贡献项为 $p\{k,\bar k\}=r\{0,0\}$，因此可知系数

$$C^{p\{0,0\}}_{12}\equiv C^p_{12}=C_{p12}$$

更进一步，由于裔场的关联函数建立在初级场的关联函数基础之上，仅当初级场相互关联时裔场相互关联，可以设想系数

$$C^{p\{k,\bar k\}}_{12}= C^p_{12}\beta_{12}^{p\{k\}}\bar \beta_{12}^{p\{\bar k\}}$$

由归一化，$\beta_{ij}^{p\{0\}}=1$，其他系数 $\beta_{ij}^{p\{k\}}$ 由算符OPE决定，为中心荷和共形维数的函数

考虑 $h_1=h_2=h$ 的简单情况，将算符OPE作用于真空

$$\phi_1(z,\bar z)\ket{h,\bar h}=\sum_p C_{p12} z^{h_p-2h}\bar z^{\bar h_p-2\bar h}\varphi(z)\bar \varphi(\bar z)\ket{h_p,\bar h_p}$$

$$\varphi(z)=\sum_{\{k\}}z^K\beta_{12}^{p\{k\}}L_{-k_1}\cdots L_{-k_n}$$

对全纯部分，以下定义态，其中 $\ket{N,h_p}$ 为Verma模 $V(h_p)$ 中的 $N$ 阶裔态

$$\ket{z,h_p}\equiv\varphi(z)\ket{h_p}=\sum_{N=0}^{\infty}z^N\ket{N,h_p}$$

$$L_0\ket{N,h_p}=(h_p+N)\ket{N,h_p}$$

对OPE左端作用 $L_n$

$$\begin{aligned}L_n\phi_1(z,\bar z)\ket{h,\bar h}&=[L_n,\phi_1(z,\bar z)]\ket{h,\bar h}\\&=\left[h(n+1) z^n+z^{n+1}\partial_z\right]\phi_1(z,\bar z)\ket{h,\bar h}\end{aligned}$$

由此关系可知 $L_n$ 对OPE右端 $\ket{z,h_p}$ 作用

$$\begin{aligned}&\sum_p C_{p12} z^{h_p-2h}\bar z^{\bar h_p-2\bar h}L_n\ket{z,h_p}\ket{\bar z,\bar h_p}\\=&\sum_p C_{p12} z^{h_p-2h}\bar z^{\bar h_p-2\bar h}\left[(h(n-1)+h_p) z^n+z^{n+1}\partial_z\right]\ket{z,h_p}\ket{\bar z,\bar h_p}\end{aligned}$$

$$L_n\ket{z,h_p}=\left[(h(n-1)+h_p) z^n+z^{n+1}\partial_z\right]\ket{z,h_p}$$

将 $\ket{z,h_p}$ 展开成级数，可得以下关系，可用其与Virasoro代数一起递归求解所有 $\ket{N,h_p}$，亦即 $\beta_{12}^{p\{k\}}$

$$L_n\ket{N+n,h_p}=(h_p+(n-1)h+N)\ket{N,h_p}$$

对于一阶裔态

$$\ket{1,h_p}=\beta_{12}^{p\{1\}}L_{-1}\ket{h_p}$$

$$L_1\ket{1,h_p}=h_p\ket{h_p}$$

$$L_1L_{-1}=L_{-1}L_1+2L_0$$

$$\beta_{12}^{p\{1\}}=\frac{1}{2}$$

对于二阶裔态

$$\ket{2,h_p}=\beta_{12}^{p\{1,1\}}L_{-1}^2\ket{h_p}+\beta_{12}^{p\{2\}}L_{-2}\ket{h_p}$$

$$L_1^2\ket{2,h_p}=h_p(h_p+1)\ket{h_p}$$

$$L_2\ket{2,h_p}=(h_p+h)\ket{h_p}$$

$$L_1 L_{-1}^2=L_{-1}^2 L_1+4L_{-1}L_0+2L_{-1}$$

$$L_1 L_{-2}=L_{-2}L_1+3L_{-1}$$

$$L_2 L_{-1}^2=L_{-1}^2L_2+6L_{-1}L_1+6L_0$$

$$L_2L_{-2}=L_{-2}L_2+4L_0+\frac{1}{2}c$$

$$\begin{pmatrix}4h_p(2h_p+1)&6h_p\\6h_p&4h_p+c/2\end{pmatrix}\begin{pmatrix}\beta_{12}^{p\{1,1\}}\\\beta_{12}^{p\{2\}}\end{pmatrix}=\begin{pmatrix}h_p(h_p+1)\\h_p+h\end{pmatrix}$$

$$\beta_{12}^{p\{1,1\}}=\frac{c-12h-4h_p+ch_p+8h_p^2}{4(c-10h_p+2ch_p+16h_p^2)}$$

$$\beta_{12}^{p\{2\}}=\frac{2h-h_p+4hh_p+h_p^2}{c-10h_p+2ch_p+16h_p^2}$$

以上利用共性对称性，得到了初级场的算符代数，尚未确定的参数仅有中心荷 $c$，初级场的共形维数和三点关联系数 $C_{pnm}$，其中 $C_{pnm}$ 需通过其他渠道例如下文的共形引导得到

共形块

利用算符代数，可递归减少关联点计算多点关联函数，考虑以下四点关联函数

$$\ev{\phi_1(z_1,\bar z_1)\phi_2(z_2,\bar z_2)\phi_3(z_3,\bar z_3)\phi_4(z_4,\bar z_4)}$$

引入交比，其在全局共形变换下保持不变

$$x=\frac{(z_1-z_2)(z_3-z_4)}{(z_1-z_3)(z_2-z_4)}\qquad \bar x=\frac{(\bar z_1-\bar z_2)(\bar z_3-\bar z_4)}{(\bar z_1-\bar z_3)(\bar z_2-\bar z_4)}$$

利用共形变换将关联点变为 $z_1=\infty,z_2=1,z_3=x,z_4=0$，四点关联函数成为

$$\lim_{z_1,\bar z_1\to\infty}z_1^{2h_1}\bar z_1^{2\bar h_1}\ev{\phi_1(z_1,\bar z_1)\phi_2(1,1)\phi_3(x,\bar x)\phi_4(0,0)}=G_{34}^{21}(x,\bar x)$$

$$G_{34}^{21}(x,\bar x)=\bra{h_1,\bar h_1}\phi_1(1,1)\phi_3(x,\bar x)\ket{h_4,\bar h_4}$$

将算符代数写为

$$\phi_3(x,\bar x)\phi_4(0,0)=\sum_p C_{34}^p x^{h_p-h_3-h_4}\bar x^{\bar h_p-\bar h_3-\bar h_4}\Psi_p(x,\bar x|0,0)$$

$$\Psi_p(x,\bar x|0,0)=\sum_{\{k,\bar k\}}\beta_{34}^{p\{k\}}\bar\beta_{34}^{p\{\bar k\}}x^K\bar x^{\bar K}\phi_p^{\{k,\bar k\}}(0,0)$$

函数 $G_{34}^{12}$ 可写为

$$G_{34}^{21}(x,\bar x)=\sum_p C_{34}^p C_{12}^p A_{34}^{21}(p|x,\bar x)$$

$$A_{34}^{21}(p|x,\bar x)=(C_{12}^p)^{-1}x^{h_p-h_3-h_4}\bar x^{\bar h_p-\bar h_3-\bar h_4}\bra{h_1,\bar h_1}\phi_1(1,1)\Psi_p(x,\bar x|0,0)\ket{0}$$

其中 $A_{kl}^{ji}$ 称为分波，可用以下图形表示，与 $(0,x)$ 到 $(1,\infty)$ 的散射过程类似

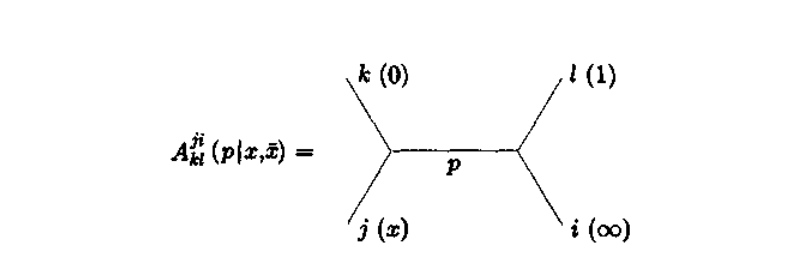
将分波进一步分解为全纯和共轭全纯两部分，其中 ${\mathcal{F}}_{34}^{21}$ 称为共形块，注意共形块表达式中分母即为 $(C_{21}^p)^{1/2}$

$$A_{34}^{21}(p|x,\bar x)={\mathcal{F}}_{34}^{21}(p|x)\bar{\mathcal{F}}_{34}^{21}(p|\bar x)$$

$${\mathcal{F}}_{34}^{21}(p|x)=x^{h_p-h_3-h_4}\sum_{\{k\}}\beta_{34}^{p\{k\}}x^K\frac{\bra{h_1}\phi_2(1)L_{-k_1}\cdots L_{-k_n}\ket{h_p}}{\bra{h_1}\phi_2(1)\ket{h_p}}$$

四点关联函数现在可写为

$$G_{34}^{21}(x,\bar x)=\sum_p C_{34}^p C_{12}^p{\mathcal{F}}_{34}^{21}(p|x)\bar{\mathcal{F}}_{34}^{21}(p|\bar x)$$

将共形块展开

$${\mathcal{F}}_{34}^{21}(p|x)=x^{h_p-h_3-h_4}\sum_{K=0}^\infty\mathcal{F}_K x^K$$

利用共形块表达式可计算系数 $\mathcal{F}_K$，由归一化知 $\mathcal{F}_0=1$，其后两个系数为

$$\mathcal{F}_1=\frac{(h_p+h_2-h_1)(h_p+h_3-h_4)}{2h_p}$$

$$\begin{aligned}\mathcal{F}_2&=\frac{(h_p+h_2-h_1)(h_p+h_2-h_1+1)(h_p+h_3-h_4)(h_p+h_3-h_4+1)}{4h_p(2h_p+1)}\\&+2\left(\frac{h_1+h_2}{2}+\frac{h_p(h_p-1)}{2(2h_p+1)}-\frac{3(h_1-h_2)^2}{2(2h_p+1)}\right)^2\left(\frac{h_3+h_4}{2}+\frac{h_p(h_p-1)}{2(2h_p+1)}-\frac{3(h_3-h_4)^2}{2(2h_p+1)}\right)^2\\&\quad\times\left(c+\frac{2h_p(8h_p-5)}{2h_p+1}\right)^{-1}\end{aligned}$$

交叉对称

由于四点关联函数中场的位置不影响关联函数(Fermion至多符号相异)，故也可将关联点变换为 $z_1=\infty,z_2=0,z_3=1-x,z_4=1$，关联函数不变

$$G_{34}^{21}(x,\bar x)=G_{32}^{41}(1-x,1-\bar x)$$

同理也可将关联点变为 $z_1=0,z_2=1,z_3=1/x,z_4=\infty$，得到

$$G_{34}^{21}(x,\bar x)=\frac{1}{x^{2h_3}\bar x^{2\bar h_3}}G_{31}^{24}(1/x,1/x)$$

以上关系称为交叉对称，将第一个关系用共形块写出

$$\sum_p C_{34}^p C_{12}^p{\mathcal{F}}_{34}^{21}(p|x)\bar{\mathcal{F}}_{34}^{21}(p|\bar x)=\sum_q C_{41}^q C_{32}^q{\mathcal{F}}_{32}^{41}(q|1-x)\bar{\mathcal{F}}_{32}^{41}(q|1-\bar x)$$

其可用图形表示为

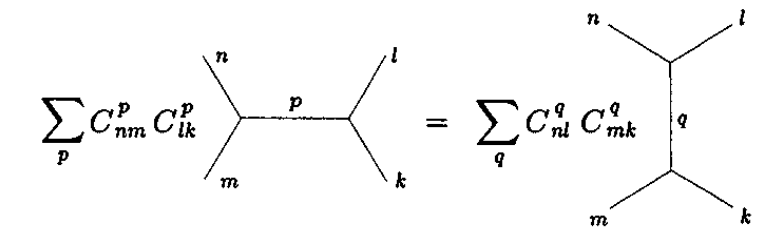
若共形块已知，则以上等式构成了对 $C_{mn}^p$ 和 $h_p$ 的约束，若有 $N$ 个共形族，则有 $N^4$ 个约束限制 $N^3+N$ 个参数 $C_{mn}^p$ 和 $h_p$，通过假定交叉对称计算关联函数的过程称为共形引导，虽然对于一般情况尚未证明共形引导等式可以完全确定理论中的参数，但对于某些特定的例子(极小模型)，等式可以完全求解，一旦通过共形不变性确定了共形块，则共形引导假设就是完全求解理论的所需的唯一“动力学输入”

从算符代数角度看，交叉对称约束十分自然，其相当于Lie代数中的Jacobi等式，并不附加更多的条件以限制理论的发展