Virasoro 示性数

对由Virasoro生成元 $L_n$ 生成的作用于最高权态 $\ket{h}$ 的Verma模 $V(c,h)$，定义生成函数 $\chi_{(c,h)}(\tau)$，称为此模的示性数，其中 $\dim(n+h)$ 为Verma模中线性独立的 $n$ 级裔数目

$$\begin{aligned}\chi_{(c,h)}(\tau)&=\Tr\; q^{L_0-c/24}\qquad(q=e^{2\pi i\tau})\\&=\sum_{n=0}^\infty\dim(h+n)q^{n+h-c/24}\end{aligned}$$

设 $p(n)$ 为可能的最大线性独立 $n$ 级裔数目，$\dim(n+h)\le p(n)$，由下式知示性数中级数在 $|q|<1$ 时一致收敛

$$\frac{1}{\varphi(q)}=\prod_{n=1}^\infty\frac{1}{1-q^n}=\sum_{n=0}^\infty p(n)q^n$$

由此一般Virasoro示性数可写为

$$\chi_{(c,h)}(\tau)=\frac{q^{h-c/24}}{\varphi(q)}$$

进一步利用Dedekind函数有

$$\eta(\tau)=q^{1/24}\varphi(q)=q^{1/24}\prod_{n=1}^\infty(1-q^n)$$

$$\chi_{(c,h)}(\tau)=\frac{q^{h+(1-c)/24}}{\eta(\tau)}$$

奇异矢量

称Verma模中能由 $L_n\;(n>0)$ 湮灭的非最高权态 $\ket{\chi}$ 为奇异矢量，其可生成 $V(c,h)$ 的子模 $V_\chi$，奇异矢量与 $V(c,h)$ 中所有态正交，包括自身

$$\bra{\chi}L_{-k_1}\cdots L_{-k_n}\ket{h}=\bra{h}L_{k_n}\cdots L_{k_1}\ket{\chi}^*=0$$

又Verma模不同级裔正交，可知 $V_\chi$ 与 $V(c,h)$ 正交，说明 $V_\chi$ 中态的模长均为零

由算符-场的对应关系，奇异态 $\ket{\chi}$ 对应奇异场 $\chi(z)$，由于 $(L_n \chi)(z)=0\;(n>0)$，$\chi(z)$ 同时为初级场与次级场

对于包含奇异矢量的Verma模，可以将其商去对应的奇异模，即将相减得到模长为零的态的两个态等同，以构造Virasoro代数的不可约表示，记为 $M(c,h)$，其为构建极小模型的基础

酉表示和Kac行列式

若Virasoro代数的表示不包含虚模长态(弦论中称为鬼场)，则称其为酉表示，由于内积只依赖于最高权 $h$ 与中心荷 $c$，要求表示为酉即为对参数 $h,c$ 施加限制条件

考虑态 $L_{-n}$ 的模长可得 $(h,c)$ 的一个简单酉边界

$$\bra{h}L_nL_{-n}\ket{h}=[2n h+\frac{1}{12}cn(n^2-1)]\bra{h}\ket{h}$$

若 $c<0$，则当 $n\to\infty$ 时模长平方为负，可见中心荷为负的表示均非酉；另外取 $n=1$ 可知共形维数 $h$ 为负的表示也均非酉

酉表示的充要条件可通过考虑以下Gram矩阵得到，将Verma模中态记为 $\ket{i}$

$$M_{ij}=\bra{i}\ket{j}\qquad (M^\dagger=M)$$

Gram矩阵为分块对角阵，$l$ 级裔态构成块 $M^{(l)}$，一般态 $\ket{a}=\sum_i a_i\ket{i}$ 的模方为

$$\braket{a}=a^\dagger M a$$

由于 $M$ 为Heimitian阵，可将其酉对角化 $M=U\Lambda U^\dagger$，记 $b=U a$

$$\braket{a}=\sum_i\Lambda_i |b_i|^2$$

因此存在虚模长态的充要条件为 $M$ 有负本征值；另外若 $M$ 有零本征值，则存在奇异矢量，Verma模可约

以下为 $l=0,1,2$ 的矩阵块 $M^{(l)}$

$$\begin{aligned}& M^{(0)}=1\\& M^{(1)}=2h\\& M^{(2)}=\begin{pmatrix} 4h(2h+1)&6h\\ 6h& 4h+c/2\end{pmatrix}\end{aligned}$$

$M^{(l)}=h$ 说明酉表示 $h>0$；接着计算 $M^{(2)}$ 的行列式与迹，酉表示要求其均为正

$$\begin{aligned}\det M^{(2)}&=32 h^3-20 h^2+4 h^2 c+ 2h c\\&=32(h-h_{1,2})(h-h_{1,2})(h-h_{2,1})\end{aligned}$$

$$\begin{aligned}& h_{1,1}=0\\& h_{1,2}=\frac{1}{16}\left(5-c-\sqrt{(1-c)(25-c)}\right)\\&h_{2,1}=\frac{1}{16}\left(5-c+\sqrt{(1-c)(25-c)}\right)\end{aligned}$$

$$\Tr M^{(2)}=8h(h+1)+c/2$$

考虑一般的Gram矩阵块 $M^{(l)}$ 的行列式，称为Kac行列式，其具有以下形式，式中 $p(n)$ 表示整数 $n$ 的配分数

$$\det M^{(l)}=\alpha_l\prod_{r,s\ge 1; rs\le l}[h-h_{r,s}(c)]^{p(l-rs)}$$

$$\alpha_l=\prod_{r,s\ge 1; rs\le l}[(2r)^s s!]^{m(r,s)}\qquad m(r,s)=p(l-rs)-p(l-r(s+1))$$

函数 $h_{r,s}$ 有多种表示，通常可写为

$$h_{r,s}(c)=h_0+\frac{1}{4}(r\alpha_++s\alpha_-)^2$$

$$h_0=\frac{1}{24}(c-1)$$

$$\alpha_\pm=\frac{\sqrt{1-c}\pm\sqrt{25-c}}{\sqrt{24}}$$

$h_{r,s}$ 的另一种表示如下，其中 $t$ 为复数，其有两支，当 $c<1\;\text{or}\; c>25$ 时，$t$ 为实数；当 $1<c<25$ 时，$t$ 位于单位圆上

$$c=13-6\left(t+\frac{1}{t}\right)$$

$$h_{r,s}(t)=\frac{1}{4}(r^2-1)t+\frac{1}{4}(s^2-1)\frac{1}{t}-\frac{1}{2}(rs-1)$$

$$t=1+\frac{1}{12}\left[1-c\pm\sqrt{(1-c)(25-c)}\right]$$

$$\alpha_+=\sqrt{t}\qquad\alpha_-=-\frac{1}{\sqrt{t}}$$

$h_{r,s}$ 还可以表示为以下形式

$$c=1-\frac{6}{m(m+1)}$$

$$h_{r,s}(m)=\frac{[(m+1)r-ms]^2-1}{4m(m+1)}$$

$$m=-\frac{1}{2}\pm \frac{1}{2}\sqrt{\frac{25-c}{1-c}}$$

$$t=\frac{m}{m+1}\quad\text{or}\quad t=\frac{m+1}{m}$$

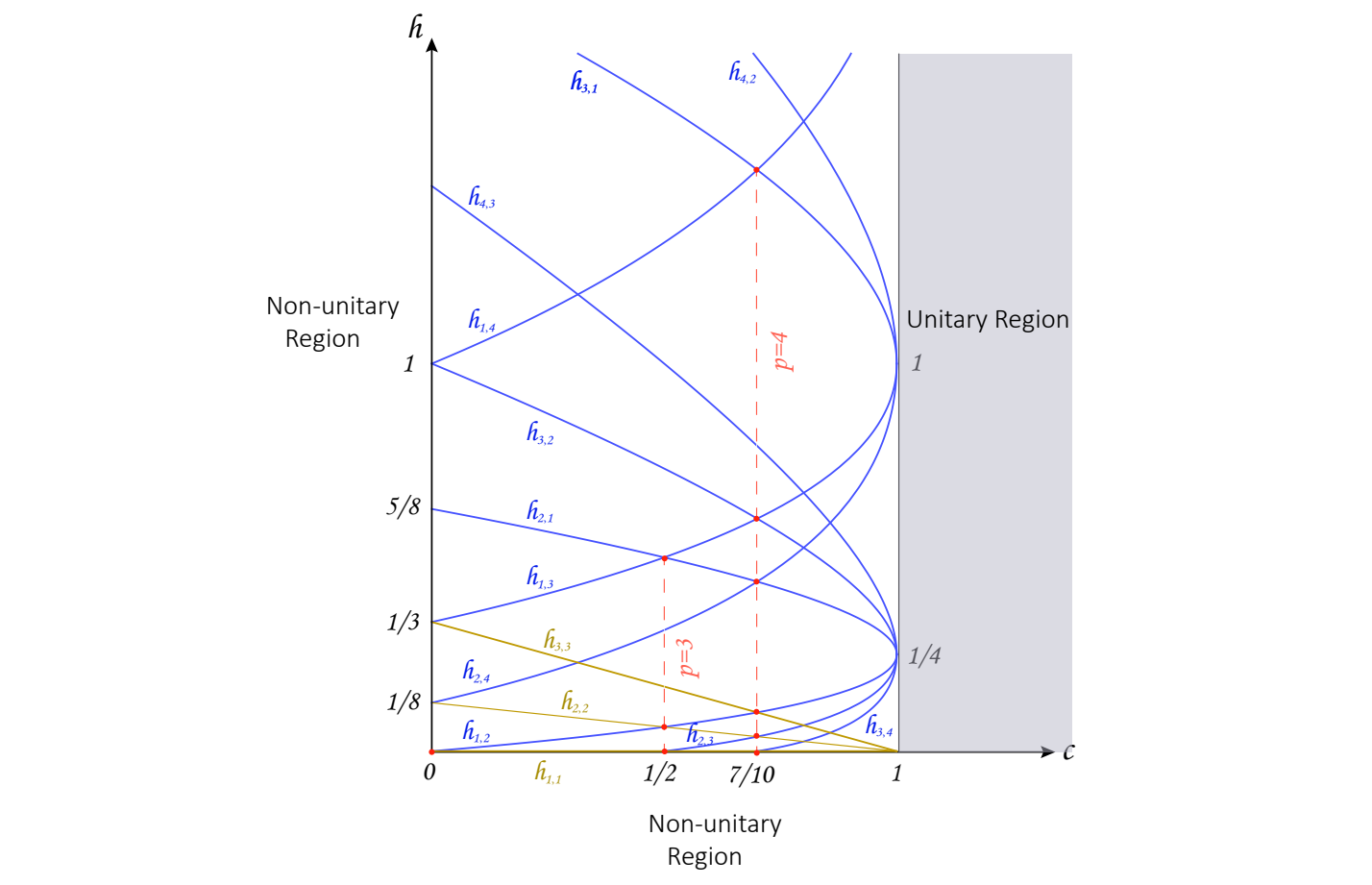
在曲线 $h=h_{r,s}(c)$ 上Kac行列式为零，称为零曲线，记作 $C_{r,s}$；对于 $l>1$，根 $h_{r,s}$ 的数目超过配分数 $p(l)$，由 $p(l-rs)=0\quad\text{for}\quad l<rs$ 结合Kac行列式一般形式知可约Verma模 $V(c,h_{r,s})$ 的第一个奇异态出现在 $l=rs$ 级矩阵块

$c\ge 1$ 酉表示

以下证明 $c\ge 1,h\ge 0$ 时表示为酉，先写出 $h_{r,s}$ 显式表达式

$$h_{r,s}(c)=\frac{1-c}{96}\left\{\left[(r+s)+(r-s)\sqrt{\frac{25-c}{1-c}}\right]^2-4\right\}$$

当 $1<c<25$ 时除 $r=s$ 外 $h_{r,s}$ 非实数，对于 $r=s$，$h_{r,s}\le 0$；当 $c\ge 25$ 时可知 $-1<m<0$，$m(m+1)<0$ 并且

$$[(m+1)r-ms]^2=[(1-|m|)r+|m|s]\ge 1$$

说明 $c> 1$ 时零曲线 $C_{r,s}$ 位于 $h=0$ 或其下方，即区域 $R=\{c>1,h>0\}$ 中Kac行列式符号相同；对给定的 $l$，取 $|h|>>\max{|h_{r,s}|}$，可得 $M^{(l)}\approx\alpha_l h^r$，由于 $\alpha_l$ 为正常数，故Kac行列式在此极限下也为正，说明 $R$ 中Kac行列式恒为正

由于 $M^{(l)}$ 负特征值数目只在穿过 $C_{r,s}$ 时改变，可知 $R$ 中其恒定且为偶数，为证明 $M^{(l)}$ 正定，只需说明其在区域中某点无负特征值，选择以下 $l$ 级裔态为基，其长度 $n(\alpha)$ 为态中算符 $L_k$ 的个数

$$L_{-k_1}L_{-k_2}\cdots L_{-k_n}\ket{h}\qquad(k_1\ge k_2\ge\cdots\ge k_n)$$

可知由 $h$ 主导的态内积的渐近行为

$$\braket{\alpha}{\alpha}=c_\alpha h^{n(\alpha)}[1+O(1/h)]$$

$$\braket{\alpha}{\beta}=O(h^{(n(\alpha)+n(\beta))/2-1})+\cdots$$

将基按长度降序排列，子矩阵 $M_n^{(l)}$ 仅由长度为 $n$ 的态内积构成，由以上渐近行为可知当 $h$ 足够大时 $M_n^{(l)}$ 正定，取极限即得 $M^{(l)}$ 正定，故 $c\ge 1,h\ge 0$ 中表示均为酉

下图绘制了酉表示区域及一些零曲线

$c< 1$ 酉表示

对于区域 $R=\{0<c<1,h>0\}$，酉表示仅存在于以下离散集中

$$c=1-\frac{6}{m(m+1)}\qquad h_{r,s}(m)=\frac{[(m+1)r-ms]^2-1}{4m(m+1)}$$

$$1\le r<m,1\le s<r,m\ge 2\qquad m,r,s\in\mathbb{Z}$$