最高权表示

单Lie代数的任何有限维不可约表示均有唯一最高权态 $\ket{\lambda}$，由非简并性知 $\ket{\lambda}$ 完全由其本征值 $\lambda(h^i)=\lambda_i$ 决定，其在单根基下的展开系数之和最大，可知对任意 $\alpha>0$，$\lambda+\alpha$ 不为权，即

$$E^{\alpha}\ket{\lambda}=0\qquad\forall\;\alpha>0$$

结合 $\lambda_i=(\lambda,\alpha_i^\vee)=-(p-q)$ 知 $p=0$，即最高权Dynkin标均大于零，为支配权

相应地对于每个支配权 $\lambda$，存在唯一有限维不可约表示 $L_\lambda$ 使其成为此表示中最高权，因此可以用最高权来指代表示，伴随表示中最高权即为最高根 $\theta$

权的重数

表示空间 $L_\lambda$ 中的所有态均可由降权算符作用于最高权态 $\ket{\lambda}$ 得到

$$E^{-\beta}E^{-\gamma}\cdots E^{-\eta}\ket{\lambda}\qquad \text{for}\quad\beta,\gamma,\eta\in\Delta_+$$

记 $L_\lambda$ 对应的权空间为 $\Omega_\lambda$，其中元素 $\lambda’$ 满足 $\lambda-\lambda’\in\Delta_+$，可知其中元素属于 $P/Q$ 中同一同余类，为寻找所有 $\lambda’\in\Omega_\lambda$，可再次利用关系

$$(\lambda’,\alpha_i^\vee)=\lambda_i ^\prime=-(p_i-q_i)\qquad p_i,q_i\in\mathbb{Z}_+ $$

权 $\lambda’$ 具有形式 $\lambda’=\lambda-\sum n_i\alpha_i\quad n_i\in\mathbb{Z}_+$，其中 $\sum n_i$ 称为权 $\lambda’$ 在表示 $\lambda$ 下的级，逐级操作可知 $n_i$ 即为 $p_i$，若 $q_i>0$ 则 $\lambda’-\alpha_i$ 也为权

由此可以得到从最高权 $\lambda$ 构造所有权的方法：对 $\lambda$ 的每个正Dynkin标 $\lambda_i>0$，构造权 $\lambda-\alpha_i,\lambda-2\alpha_i,\cdots,\lambda-\lambda_i\alpha_i$，然后用得到的新权代替最高权 $\lambda$ 重复以上过程，直到构造出的权无正Dynkin标为止，以下为 $\mathfrak{su}(3)$ 和 $\mathfrak{sp}(4)$ 伴随表示中权的构造

$\mathfrak{su}(3)$

$\mathfrak{sp}(4)$

权的重数可用以下Freudenthal递归公式计算，其来历将在下文说明

$$[|\lambda+\rho|^2-|\lambda’+\rho|^2]\text{mult}_\lambda(\lambda’)=2\sum_{\alpha>0}\sum_{k=1}^\infty(\lambda’+k\alpha,\alpha)\text{mult}_\lambda(\lambda’+k\alpha)$$

以 $\mathfrak{su}(3)$ 伴随表示为例，递归计算可知正权的重数均为 $1$，而零权的重数

$$(8-2)\text{mult}_\theta(0,0)=2\times 2(1+1+1)\quad\Longrightarrow\quad \text{mult}_\theta(0,0)=2$$

事实上伴随表示中零权的重数等于代数的秩 $r$，而非零权非简并

$W$ 轨道中的权重数均相同，其反映了单根基的任意性，即固定 $w$，$\{w\alpha_i\}$ 可作为基

$$\text{mult}_\lambda(w\lambda’)=\text{mult}_\lambda(\lambda’)\qquad\forall\; w\in W$$

由最高权Dynkin标均为正可知有限维不可约表示模 $L_\lambda$ 总为酉，即配备 $(H^i)^\dagger=H^i$，$(E^\alpha)^\dagger=E^{-\alpha}$，$L_\lambda$ 中态 $\ket{\lambda’}$ 的自内积均正定，此性质对态的线性组合也成立

$$\braket{\lambda’}{\lambda’}=\bra{\lambda}E^\gamma\cdots E^\beta E^{-\beta}\cdots E^{-\gamma}\ket{\lambda}>0$$

共轭表示

在有限维不可约表示中，存在唯一最低态，其在最高态 $\lambda$ 的 $W$ 轨道之中，其腔位于基本腔的正对面，若Weyl群中最长元素为 $w_0$，则最低态为 $w_0\lambda$

将表示 $\lambda$ 作以下颠倒可得其共轭表示 $\lambda^*$，由 $\rho$ 为自共轭表示 $\rho=-w_0\rho$ 中最高权，可知共轭表示中最高权态即为原表示中的负最低态 $\lambda^*=-w_0\lambda$

$$\lambda^*=(-w_0)\cdot\lambda\equiv -w_0(\lambda+\rho)-\rho$$

对于 $\mathfrak{su}(N)$，其最长元素为

$$w_0=s_1s_2\cdots s_{N-1}s_1 s_2\cdots s_{N-2}s_1s_2s_1$$

取 $N=3$，权在共轭表示中的对应为

$$(-w_0)\cdot(\lambda_1,\lambda_2)=-s_1s_2s_1(\lambda_1+1,\lambda_2+1)-(1,1)=(\lambda_2,\lambda_1)$$

共轭与Dynkin图的反射对称有关，对于 $\mathfrak{su}(N)$，共轭即为将权的Dynkin标逆序排列；由于 $\mathfrak{so}(2r+1)$，$\mathfrak{sp}(2r)$，$\mathfrak{so}(4r)$，$G_2$，$F_4$，$E_7$ 的Dynkin图无对称性，故其表示均自共轭，其他代数的自共轭表示中最高权需满足以下条件

$$\begin{array}{l}&\mathfrak{su}(r+1):&\quad&\lambda_i=\lambda_{r-i}\\&\mathfrak{so}(4r+2):&\quad&\lambda_r=\lambda_{r+1}\\&E_6:&\quad&\lambda_1=\lambda_5,\quad \lambda_2=\lambda_4\end{array}$$

二次Casimir算符

记基 $\{\mathcal{L}^a\}$ 下由Killing形式确定的度规为 $g^{ab}=K(\mathcal{L}^a,\mathcal{L}^b)$，定义二次Casimir算符

$$\mathcal{Q}=g_{ab}\mathcal{L}^a \mathcal{L}^b$$

在标准基 $\{J^a\}$ 下

$$\mathcal{Q}=\sum_a J^a J^a$$

在Cartan-Weyl基下

$$\mathcal{Q}=\sum_i H^i H^i+\sum_{\alpha>0}\frac{|\alpha|^2}{2}(E^\alpha E^{-\alpha}+E^{-\alpha}E^\alpha)$$

注意到 $\mathcal{Q}$ 并不是 $\mathfrak{g}$ 中元素，其位于 $\mathfrak{g}$ 的泛包络代数，即 $\mathfrak{g}$ 中元素的形式幂级数集中

由度规对称性可知 $\mathcal{Q}$ 与代数中所有生成元对易，其本征值对不可约表示中所有态均相同，以下在Cartan-Weyl基下对最高权态计算此本征值

$$\sum_{i}H^i H^i\ket{\lambda}=\sum_i\lambda^i\lambda^i\ket{\lambda}=(\lambda,\lambda)\ket{\lambda}$$

$$[E^\alpha,E^{-\alpha}]\ket{\lambda}=\frac{2}{|\alpha|^2}\alpha\cdot H\ket{\lambda}=\frac{2}{|\alpha|^2}(\alpha,\lambda)\ket{\lambda}$$

可知

$$\mathcal{Q}\ket{\lambda}=[(\lambda,\lambda)+\sum_{\alpha>0}(\alpha,\lambda)]\ket{\lambda}=(\lambda,\lambda+2\rho)\ket{\lambda}$$

在伴随表示中，二次Casimir算符的本征值即为对偶Coxeter数的两倍

$$\begin{aligned}(\theta,\theta+2\rho)&=2+2(\theta,\rho)=2+2\sum_{i,j}a_i^\vee(\alpha_i^\vee,\omega_j)\\&=2+2\sum_i a_i^\vee=2g\end{aligned}$$

二次Casimir算符不区分表示与其共轭

$$\mathcal{Q}\ket{\lambda^*}=\mathcal{Q}\ket{\lambda}$$

由此可知下式成立，其也可由共轭表示的定义直接得到

$$|\lambda^*+\rho|^2=|\lambda+\rho|^2$$

Freudenthal递归公式可由在与权 $\lambda’$ 相关的子空间计算 $\mathcal{Q}$ 的迹得到

对于 $\mathfrak{su}(2)$，二次Casimir算符为唯一与所有生成元对易的算符，但对于高秩代数，相应地存在高次Casimir算符，其次减一称为代数的幂；对于单缀Lie代数，幂可由邻接矩阵 $G_{ij}=2-A_{ij}$ 的本征值 $2\cos(n_i\pi/g)$ 简单定义，其中 $n_i$ 即为幂

表示的指标

考虑不变双线性形式 $\Tr_\lambda(\mathcal{R}(J^a)\mathcal{R}(J^b))$ 的归一化，其中 $\mathcal{R}(J^a)$ 代表生成元 $J^a$ 的表示，迹在 $L_\lambda$ 中计算，对此形式作如下对应于 $|\theta|^2$ 的归一化，其定义了表示 $\lambda$ 的Dynkin指标 $x_\lambda$

$$\Tr_\lambda(\mathcal{R}(J^a)\mathcal{R}(J^b))=|\theta|^2x_\lambda\delta_{ab}=2x_\lambda\delta_{ab}$$

取 $a=b$，对所有 $a$ 求和，等式左边即为Casimir算符的迹，可得 $x_\lambda$ 的显式表达式

$$x_\lambda=\frac{\dim|\lambda|(\lambda,\lambda+2\rho)}{2\dim \mathfrak{g}}$$

在伴随表示下 $\dim |\theta|=\dim \mathfrak{g}$，$(\theta,\rho)=g-1$，Dynkin指标即为Coxeter数

$$x_\theta=g$$

表与型

此节介绍最高权的图形表示，其也为张量积计算中的有效工具，此图形表示的改进可导出有限维表示中态的完整基构造；下文也将说明此图形表示等价于所谓Gelfand-Tsetlin型，其用三角数阵列描述态，为简单起见，下文讨论仅局限于 $\mathfrak{su}(N)$

Young表

考虑 $\mathfrak{su}(N)$ 可积最高权 $\lambda$，其Dynkin标为

$$\lambda=(\lambda_1,\cdots,\lambda_{N-1})$$

其也可由以下配分等价描述

$$\lambda=\{l_1;l_2;\cdots;l_{N-1}\}$$

$$l_i=\lambda_i+\lambda_{i+1}+\cdots+\lambda_{N-1}$$

对此配分可关联相应的Young表，其由左对齐方格阵列组成，其中第 $i$ 行的方格数为 $l_i$

以 $\mathfrak{su}(5)$ 中权为例，其Young表如下所示

$$\lambda=(2,0,2,0)=\{4;2;2\}$$

Dynkin标提供了此表的对偶描述：$\lambda_i$ 为列方格数等于 $i$ 的列数

基本表示 $\omega_l$ 由方格数为 $l$ 的单列描述，而方格数为 $N$ 的列对应标量表示，为无效表；若允许方格数为 $N$ 的列存在，则配分由 $N$ 个整数确定，当 $l_N\neq 0$，总能从配分中减去 $\{l_N;l_N;\cdots;l_N\}$，即从表中消除方格数为 $N$ 的列，$l_N=0$ 的表称为约化表，例如

$$\{5;3;3;1;1\}=\{4;2;2\}$$

可将Young表作类似于矩阵的转置，记转置后的表对应的权为 $\lambda^t$，例如

配分与正交基

$\mathfrak{su}(N)$ 中元素可用 $N\times N$ 无迹矩阵表示，Cartan子代数由所有无迹对角阵张成；令 $e_{ij}$ 表示除 $(i,j)$ 位置为 $1$ 外其余位置均为 $0$ 的矩阵，Cartan 子代数中元素可表示为 $\sum_{i=1}^N\epsilon_i e_{ii},\sum_{i=1}^N\epsilon_i=0$，梯算符为 $e_{ij},i\neq j$，可知根为 $\epsilon_i-\epsilon_{j}$，一组单根基为

$$\alpha_i=\epsilon_i-\epsilon_{i+1}\qquad i=1,\cdots,N-1$$

将 $\epsilon_i$ 视作 $r+1$ 维空间中的正交矢量，可知根阵为

$$Q=\sum_{i=1}^N n_i\epsilon_i\qquad n_i\in\mathbb{Z},\sum_{i=1}^N n_i=0$$

由 $\epsilon_i^2=1$，$\epsilon_i\cdot\epsilon_j=0\;\text{for}\;i\neq j$ 可知 $|\alpha|^2=2,\;\forall\;\alpha\in Q$，根与伴根相同，基本权与单根通过二次型矩阵相联系

$$\omega_i=\epsilon_1+\epsilon_2+\cdots+\epsilon_i-\frac{i}{N}\sum_{i=1}^N\epsilon_i$$

可见最高权在 $\{\epsilon_i\}$ 基下的展开系数即为配分数

$$\lambda=\sum_{i=1}^{N-1}\lambda_i\omega_i=\sum_{i=1}^N(l_i-\kappa)\epsilon_i\qquad \kappa=\frac{1}{N}\sum_{j=1}^{N-1}j\lambda_j$$

由最高权减去单根 $\epsilon_i-\epsilon_j,i<j$ 可得其他权，以上构造给出其在 $\{\epsilon_i\}$ 基下的展开系数，因此权 $\lambda’$ 也可由配分 $\{l_1’;l_2’;\cdots;l_N’\}$ 描述，但非最高权的配分与Young表的形状并无关联

半标准表

现在说明表可用以显式描述表示中的所有态，此过程需要用正整数填充Young表中的方格形成所谓半标准表，其定义如下

令 $c_{i,j}$ 为填充Young表 $i$ 行 $j$ 列方格的整数，其从左到右非减，从上到下严格递增

$$1\le c_{i,j}\le N\qquad c_{i,j}\le c_{i,j+1}\qquad c_{i,j}<c_{i+1,j}$$

具有形状 $\lambda$ 的半标准表与 $L_\lambda$ 中态一一对应，半标准表中的数字蕴含相应权的配分信息，表中 $i$ 的数量即为权 $\lambda’=\{l_1’;l_2’;\cdots;l_N’\}$ 中 $l_i’$；对于最高权，第 $i$ 行中所有方格均填充 $i$；将填充 $i$ 的方格视为 $\epsilon_i$，半标准表对应的权即为将所有方格相加

$$\epsilon_i=\omega_i-\omega_{i-1}\qquad i=1,\cdots,N$$

$$(\text{modulo}\;\sum \epsilon_i/N)\qquad \omega_0=\omega_N=0$$

给定配分可以构造的固定形状的半标准表的数量给出此表示下对应权的重数，换言之，构造半标准表的规则提供了Freudenthal重数公式的组合学实现

以 $\mathfrak{su}(3)$ 为例，表示 $\omega_1$ 下三个态的半标准表为

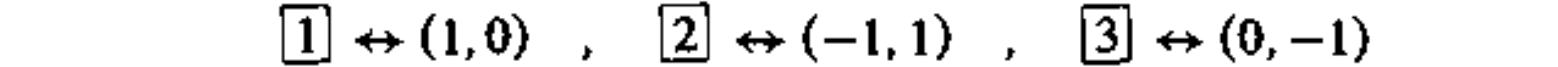
表示 $\omega_2$ 下三个态的半标准表为

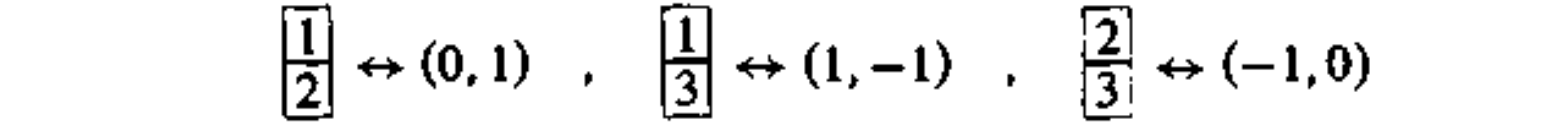
伴随表示 $(1,1)$ 包含 $8$ 个半标准表，可见权 $(0,0)$ 重数为 $2$

而 $\mathfrak{su}(4)$ 表示 $(2,0,2)$ 下权 $(0,0,0)=\{2;2;2;2\}$ 重数为 $6$

Gelfand-Tsetlin型

与半标准表基等价的表示可由Gelfand-Tsetlin型给出，对给定的半标准表关联以下三角阵列，其中 $\beta_i^{(j)}$ 为第 $i$ 行中格内数字小于等于 $j$ 的方格数

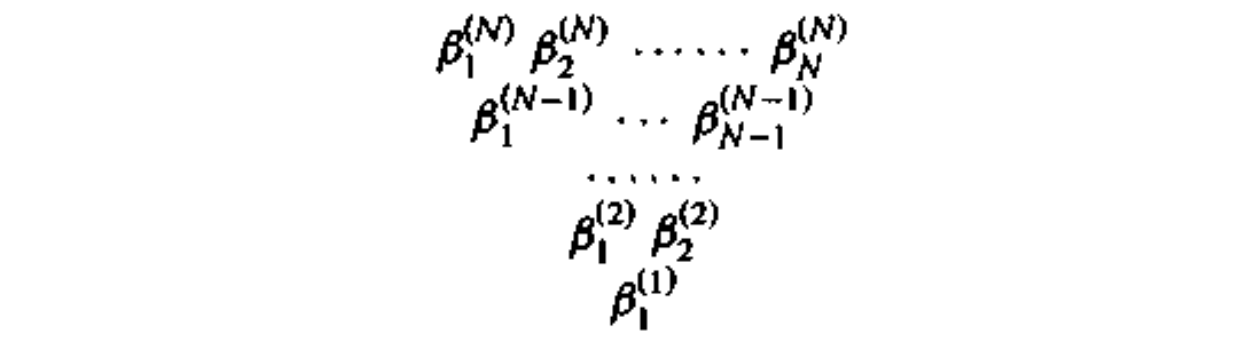
以下为 $\mathfrak{su}(4)$ 表示 $(1,2,1)$ 下权 $(-2,1,0)$ 对应的半标准表和Gelfand-Tsetlin型

表示中的所有Gelfand-Tsetlin型的第一行均相同，为表形状的配分

$$\beta_i^{(N)}=l_i$$

确定第一行后，按以下规则填充三角阵列可得表示中的所有态

$$\beta_i^{(j)}\ge \beta_{i+1}^{(j)}\qquad\beta_i^{(j)}\ge\beta_{i+1}^{(j+1)}$$

$\mathfrak{su}(3)$ 表示 $(1,1)$ 下的 $8$ 个型为

表示下的最高权态的Gelfand-Tsetlin型可由配分完全确定，为

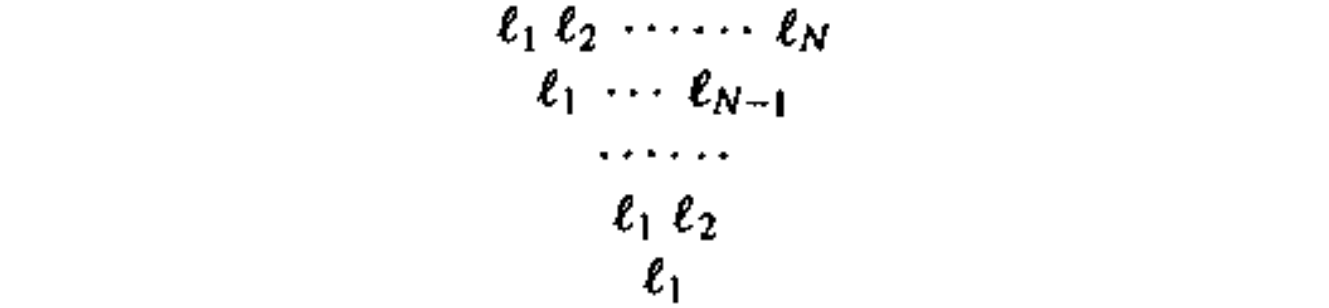
特征标

Weyl特征标公式

最高权 $\lambda$ 表示的形式特征标定义如下

$$\chi_\lambda=\sum_{\lambda’\in\Omega_\lambda}\text{mult}_\lambda(\lambda’)e^{\lambda’}$$

其中 $e^\lambda$ 为满足以下条件的形式指数，第二个等式右边的 $e$ 为真正的指数函数，$\xi$ 为对偶Cartan子代数中的任意元素，即任意权

$$e^\lambda e^\mu=e^{\lambda+\mu}$$

$$e^\lambda(\xi)=e^{(\lambda,\xi)}$$

下文说明形式特征标与表示论中的特征标的关系，令 $G$ 为 $\mathfrak{g}$ 对应的Lie群，$H$ 为 $G$ Cartan子群中的元素，$H$ 在某表示下的特征标即为在对应模 $V$ 中简单取迹

$$\Tr_V H=\sum_\gamma\text{mult}(\gamma)[\gamma(H)]$$

其中 $\gamma(H)$ 表示 $H$ 的本征值，将 $H$ 写为Cartan子代数中元素的指数形式 $H=\exp(h)$，将单个元素 $h$ 替换为矢量 $\tilde{h}=(h^1,h^2,\cdots,h^r)$ 可张成完整Cartan子群，对应 $\gamma(H)$ 替换为 $e^{\lambda’(\tilde{h})}=e^{(\lambda_1’,\cdots,\lambda_r’)}$，$\lambda’$ 即为权；对于矢量指数，$e$ 需视作形式指数函数

以上 $\chi_\lambda$ 的表达式可经过两步操作化为更易处理的形式，下文忽略操作过程的细节，首先引入辅助量

$$D_\rho=\prod_{\alpha>0}(e^{\alpha/2}-e^{-\alpha/2})$$

可以证明 $D_\rho$ 实际上为以下对Weyl群元的求和

$$D_\rho=\sum_{w\in W}\epsilon(w)e^{w\rho}$$

第二步更为复杂，为利用Freudenthal重数公式证明下式

$$D_\rho\chi_\lambda=D_{\lambda+\rho}$$

此即著名的Weyl特征标公式

$$\chi_\lambda=\frac{D_{\lambda+\rho}}{D_\rho}=\frac{\displaystyle\sum_{w\in W}\epsilon(w)e^{w(\lambda+\rho)}}{\displaystyle\sum_{w\in W}\epsilon(w)e^{w\rho}}$$

对于 $\mathfrak{su}(2)$，记 $t=e^{\omega_1}$，其特征标为

$$\chi_\lambda=\frac{t^{\lambda_1+1}-t^{-\lambda_1-1}}{t-t^{-1}}=t^{\lambda_1}+t^{\lambda_1-2}+\cdots+t^{-\lambda_1}$$

对于某些操作，考虑特征标与特定值 $\xi$ 的计算结果会更为方便

$$\chi_\lambda(\xi)=\frac{\displaystyle\sum_{w\in W}\epsilon(w)e^{(w(\lambda+\rho),\xi)}}{\displaystyle\sum_{w\in W}\epsilon(w)e^{(w\rho,\xi)}}$$

维数与奇异公式

应用特征标公式可导出表示的维数公式，易知 $\chi_\lambda(0)$ 即为表示维数，但由于 $\sum\epsilon(w)=0$，不能直接取 $\xi=0$，故令 $\xi=t\rho$，考虑 $t\to 0$ 的极限情况

$$\chi_\lambda(t\rho)=\frac{D_{\lambda+\rho}(t\rho)}{D_\rho(t\rho)}=\frac{D_\rho(t(\lambda+\rho))}{D_\rho(t\rho)}=\prod_{\alpha>0}\frac{\sinh(\alpha,(\lambda+\rho)t/2)}{\sinh(\alpha,\rho t/2)}$$

由上式即得维数公式

$$\dim|\lambda|=\lim_{t\to 0}\chi_\lambda(t\rho)=\prod_{\alpha>0}\frac{(\lambda+\rho,\alpha)}{(\rho,\alpha)}$$

对 $\mathfrak{su}(2)$，$\mathfrak{su}(3)$，$\mathfrak{sp}(4)$ 应用维数公式

$$\begin{array}{l}
& \mathfrak{su}(2):&&\dim|\lambda|=\lambda_1+1\\
& \mathfrak{su}(3):&&\dim|\lambda|=\displaystyle\frac{1}{2}(\lambda_1+1)(\lambda_2+1)(\lambda_1+\lambda_2+2)\\
& \mathfrak{sp}(4):&&\dim|\lambda|=\displaystyle\frac{1}{6}(\lambda_1+1)(\lambda_2+1)(\lambda_1+2\lambda_2+3)(\lambda_1+\lambda_2+2)\\
\end{array}$$

将 $\chi_\lambda(t\rho)$ 展开至 $t$ 的非零主导项

$$\begin{aligned}\chi_\lambda(t\rho)&=\prod_{\alpha>0}\frac{(\lambda+\rho,\alpha)}{(\rho,\alpha)}\left\{1+\frac{t^2}{24}[(\alpha,\lambda+\rho)^2-(\alpha,\rho)^2]\right\}\\ &=\dim|\lambda|\left\{1+\frac{t^2}{24}\sum_{\alpha>0}[(\alpha,\lambda+\rho)^2-(\alpha,\rho)^2]\right\}\end{aligned}$$

利用下式，其将在下文证明，其中 $y$ 为与代数有关的常数

$$(\lambda,\mu)=\frac{1}{y}\sum_{\alpha\in\Delta}(\lambda,\alpha)(\alpha,\mu)=\frac{2}{y}\sum_{\alpha\in\Delta_+}(\lambda,\alpha)(\alpha,\mu)$$

特征标展开式化为

$$\chi_\lambda(t\rho)=\dim|\lambda|\left\{1+\frac{t^2 y}{48}[|\lambda+\rho|^2-|\rho|^2]\right\}$$

写出特征标定义展开式

$$\chi_\lambda(t\rho)=\sum_{\lambda’\in\Omega_\lambda}\text{mult}_\lambda(\lambda’)e^{(\lambda’,\rho)t}$$

二者比较可知

$$\frac{1}{2}\sum_{\lambda’\in\Omega_\lambda}\text{mult}_\lambda(\lambda’)(\lambda’,\rho)^2=\frac{y}{48}\dim|\lambda|\;[|\lambda+\rho|^2-|\rho|^2]$$

对于伴随表示 $\lambda=\theta$，非零权 $\lambda’$ 为重数为 $1$ 的根，等式左边化为

$$\frac{1}{2}\sum_{\lambda’\in\Omega_\theta}\text{mult}_\theta(\lambda’)(\lambda’,\rho)^2=\frac{1}{2}\sum_{\alpha\in\Delta}(\rho,\alpha)(\alpha,\rho)=\frac{1}{2}y|\rho|^2$$

而 $\dim|\theta|=\dim\mathfrak{g}$，$(\theta,\rho)=g-1$，等式右边为

$$\frac{y}{48}\dim|\theta|(\theta,\theta+2\rho)=\frac{yg}{24}\dim\frak{g}$$

结合即得Freudenthal-de Vries奇异公式

$$|\rho|^2=\frac{g}{12}\dim\mathfrak{g}$$

回到等式 $\displaystyle(\lambda,\mu)=\frac{1}{y}\sum_{\alpha\in\Delta}(\lambda,\alpha)(\alpha,\mu)$ 的证明，考虑算符 $\displaystyle\sum_{\alpha\in\Delta}\alpha\alpha^t$，其中 $\alpha^t$ 表示 $\alpha$ 的转置，由于Weyl群元的作用为对根集的置换，故此算符与Weyl群中所有元素对易，又Weyl群对 $\displaystyle\sum_{\alpha\in\Delta}\alpha\alpha^t$ 的作用不可约，故其正比于单位阵，左右内积即得所需证明

$$\sum_{\alpha\in\Delta}\alpha\alpha^t=yI_r$$

继续对上式求迹可得

$$\sum_{\alpha\in\Delta}|\alpha|^2=yr$$

等式左边可由上文中Dynkin指标定出

$$\Tr_\theta H^i H^j=2g\delta^{ij}$$

取 $j=i$，对 $i$ 求和可得

$$\sum_i\sum_{\alpha\in\Delta}\alpha^i\alpha^i=\sum_{\alpha\in\Delta}|\alpha|^2=2gr$$

由此确定常数 $y$ 为对偶Coxeter数的两倍

$$y=2g$$

Schur方程

在上文的 $\mathfrak{su}(N)$ 正交基 $\{\epsilon_i\}$ 下，特征标称为Schur方程，在此基下可得表示维数的一个简单组合学方程

在正交基下，Weyl群的作用相当于 $N$ 个基矢量的置换群 $S_N$，反射 $s_\alpha,\;\alpha=\epsilon_i-\epsilon_j$ 的作用即为交换 $\epsilon_i$ 和 $\epsilon_j$，利用此性质可将特征标写为矩阵行列式之比，即Schur方程

引入以下变量

$$q_i=e^{\epsilon_i}\qquad\prod_{i=1}^N q_i=1$$

形式指数可写为

$$e^\lambda=q_1^{l_1}q_2^{l_2}\cdots q_N^{l_N}$$

$D_\lambda$ 可写为

$$D_\lambda=\sum_{w\in W}\epsilon(w)e^{w\lambda}=\sum_{\sigma\in S_N}\epsilon(\sigma)\prod_{i=1}^N q^{l_{\sigma(i)}}=\det q_j^{l_i}$$

由 $\rho$ 配分的第 $i$ 个数为 $N-i$，特征标可写作以下形式，其中 $S_\lambda$ 即代表Schur方程

$$\chi_\lambda=S_\lambda(q_1,\cdots,q_N)=\frac{\det q_j^{l_i+N-i}}{\det q_j^{N-i}}$$

上式分母即为Vandermonde行列式

$$\det q_j^{N-i}=\pm \det q_j^{i-1}=\pm\det\begin{pmatrix}
1&1&\cdots&1\\
q_1&q_2&\cdots&q_N\\
\vdots&&&\\
q_1^{N-1}& q_2^{N-1}&\cdots&q_N^{N-1}
\end{pmatrix}$$

$$\det q_j^{N-i}=\pm \prod_{1\le i< j\le N}(q_i-q_j)$$

同样令 $q_i\to 1$ 可得维数公式

$$\dim|\lambda|=\prod_{1\le i< j\le N}\frac{l_i-l_j+j-i}{j-i}$$