复向量空间与复流形
上维复向量丛由拓扑空间和映射构成,其纤维为维复平面,且满足局部平凡条件:上每点具有邻域,其原像同胚于,此同胚将每点纤维复线性地映为
维复向量丛可由对维实向量丛施加复结构[得到,所谓复结构即为连续映射
其将总空间实线性地映为自身,此复结构可将每点纤维变为复向量空间
易验证其满足局部平凡条件,故成为复丛。反之也可由复丛去掉复结构得到潜在实丛
切丛令为开子集,则切丛与总空间具有以下正则复结构
考虑开集之间的光滑映射,,实线性映射对所有复线性的条件为
此即Cauchy-Riemann方程,说明复切丛的局部平凡条件要求底流形同胚为全纯函数
令为维光滑流形,切丛上的复结构有时称为上的近复结构,此近复结构成为上复结构的条件为:上每点均具有同胚于中开集的开邻域,且此同胚的导数处处满足复线性条件,即
此时称为具有复维数的复流形,简写为。令为两个复流形之间的光滑映射,若满足,则称全纯
一个基本定理断言上的近复结构成为复结构的充要条件为
对光滑流形施加复结构的最经典的过程如下:首先选定一组同胚,其中为中开集,为开覆盖,只需验证下列每个复合映射全纯即可
陈类
引理1若为复向量丛,则其潜在实向量丛具有典范定向
此引理的证明只需注意到为联通群,因此维复空间中任意一组基均可通过连续形变成为任意另一组基,此过程保持潜在实空间定向不变,即其定向不依赖于基的选取。将此引理应用于切丛可知任意复流形均具有一个典范定向
对于底空间上的维复平面丛,其Euler class 具有良好定义,若为相同底空间上的维复平面丛,则有
这可由两个复向量丛纤维的典范定向诱导出的典范定向得出,即作为可定向丛同胚于
Hermitian度规
复向量丛上的Hermitian度规是满足如下条件的潜在实丛上的Euclidean度规
给定上Hermitian度规,对相同纤维上向量,容易证明有且仅有一个复值内积满足条件:双复线性,,其形式为
复值内积满足,若,则称正交。若底空间仿紧,则其上每一个复向量丛均容许Hermitian度规
陈类构造
构造维复向量丛的示性类,首先需构造删除总空间上的典范维平面丛
中的点由的一个纤维与此纤维中的一个非零向量决定,若上已经确定了Hermitian度规,则在处的纤维即为中与正交的成分;若不使用Hermitian度规,也可定义在处的纤维为商空间,其中为非零向量张成的一维子空间,这两种构造的纤维典范同构
由于任意实定向维平面丛均具有下列整系数正合Gysin序列
可知对于,为同构
陈类 可由对的维数归纳定义,首先定义顶陈类为Euler class
对于,由于为同构,故定义
对于,定义陈类为零。总陈类为环中形式和,其逆具有良好定义
引理2(Naturality)若被由上的维复平面丛到上的维复平面丛的丛映射覆盖,则
此引理可由对归纳证明,由于Euler class自然,故顶陈类满足
对于低阶陈类,注意到丛映射诱导出
此映射被维丛映射覆盖,归纳可知
由以下交换图和同胚即得引理证明
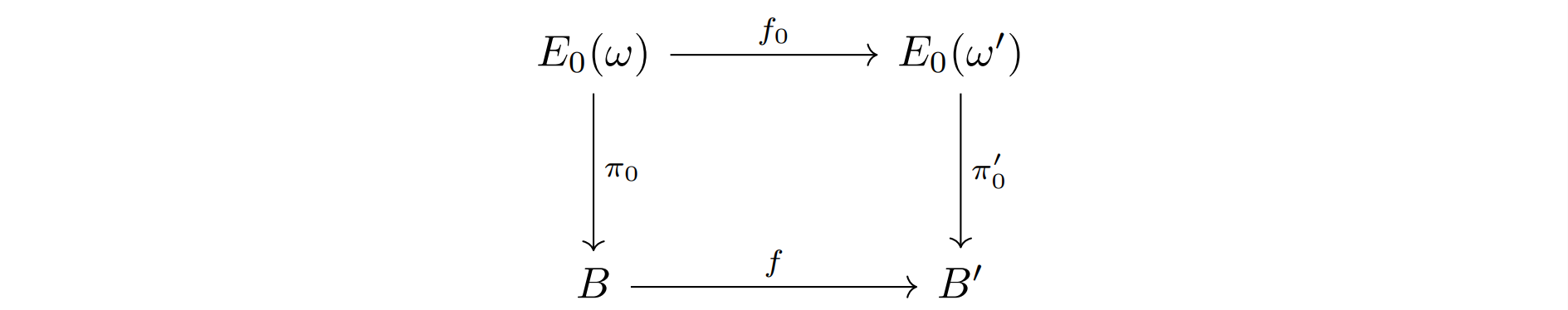
引理3若为上的平凡复平面丛,则
只需证明的情况,令为维复平面丛,由于含有一个非零截面,故顶陈类;令为此截面,其被丛映射覆盖,故,而,,引理得证
复Grassmann流形
复Grassmann流形为中所有经过原点的维复平面的集合,其具有维复解析流形的自然结构